3.3 Differential Kinematics in 3D (2)

---

3.3.1 Revisit to 3R Planar Manipulator

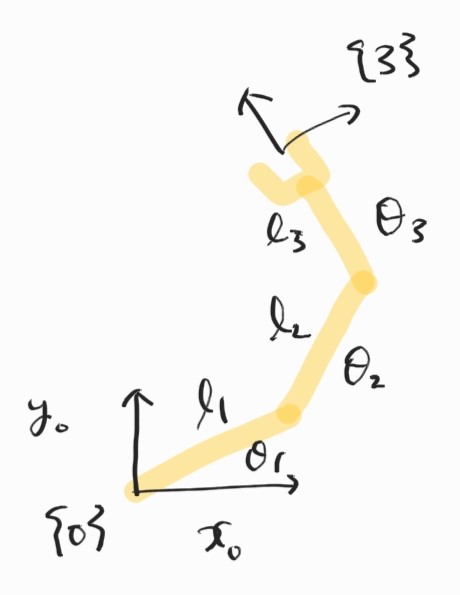
Jacobian부터 구하자.

먼저 Forward kinematics.

\[x = l_1c_1 + l_2c_{12} + l_3c_{123} \\ y = l_1s_1 + l_2s_{12} + l_3s_{123} \\ \alpha = \theta_1 + \theta_2 + \theta_3\]

미분.

\[\dot{x} = -(l_1s_1 + l_2s_{12} + l_3s_{123})\dot{\theta}_1 - (l_2s_{12} + l_3s_{123}) \dot{\theta}_2 - l_3s_{123} \dot{\theta}_3 \\ \dot{y} = (l_1c_1 + l_2c_{12} + l_3c_{123})\dot{\theta}_1 + (l_2c_{12} + l_3c_{123}) \dot{\theta}_2 + l_3c_{123} \dot{\theta}_3 \\ \dot{\alpha} = \dot{\theta}_1+\dot{\theta}_2+\dot{\theta}_3\]

Matrix form으로는

\[\dot{\textbf{X}} = \textbf{J}(\boldsymbol{\theta})\dot{\boldsymbol{\theta}}\] \[\begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\alpha} \end{bmatrix} = \begin{bmatrix} -(l_1s_1 + l_2s_{12} + l_3s_{123}) & - (l_2s_{12} + l_3s_{123}) & - l_3s_{123} \\ l_1c_1 + l_2c_{12} + l_3c_{123} & l_2c_{12} + l_3c_{123} & l_3c_{123} \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} \dot{\theta}_1 \\ \dot{\theta}_2 \\ \dot{\theta}_3 \end{bmatrix}\]

---

3.3.2 Interpretations of Jacobian

\[\textbf{J}(\boldsymbol{\theta}) = \begin{bmatrix} \frac{\partial x}{\partial \theta_1} & \frac{\partial x}{\partial \theta_2} & \frac{\partial x}{\partial \theta_3} \\ \frac{\partial y}{\partial \theta_1} & \frac{\partial y}{\partial \theta_2} & \frac{\partial y}{\partial \theta_3} \\ \frac{\partial \alpha}{\partial \theta_1} & \frac{\partial \alpha}{\partial \theta_2} & \frac{\partial \alpha}{\partial \theta_3} \\ \end{bmatrix} = \begin{bmatrix} -(l_1s_1 + l_2s_{12} + l_3s_{123}) & - (l_2s_{12} + l_3s_{123}) & - l_3s_{123} \\ l_1c_1 + l_2c_{12} + l_3c_{123} & l_2c_{12} + l_3c_{123} & l_3c_{123} \\ 1 & 1 & 1 \end{bmatrix}\] \[\dot{\textbf{X}} = \textbf{J}\dot{\boldsymbol{\theta}} = \textbf{J}_1\dot{\theta}_1 + \textbf{J}_2\dot{\theta}_2 + \textbf{J}_3\dot{\theta}_3\] \[\textbf{J} = \begin{bmatrix} \textbf{J}_1 & \textbf{J}_2 & \textbf{J}_3 \end{bmatrix}\]

즉, velocity는 Jacobian의 column space이다. 각 joint velocity부터 end-effector velocity까지의 contribution을 찾을 수 있다.

그런데, 만약 derivative를 찾지 못하면 어쩌지?

---

3.3.3 Computation of Jacobian

일반적인 manipulator는 Jacobian이 end-effector의 linear/angular velocity와 joint의 velocity를 연관짓는다.

\[\boldsymbol{\nu} = \begin{bmatrix} \textbf{v} \\ \boldsymbol{\omega} \end{bmatrix} = \begin{bmatrix} \textbf{J}_v \\ \textbf{J}_{\omega} \end{bmatrix} \dot{\boldsymbol{\theta}} = \textbf{J}(\boldsymbol{\theta})\dot{\boldsymbol{\theta}}\] \[\textbf{v} = \textbf{J}_v \dot{\boldsymbol{\theta}} \\ \boldsymbol{\omega} = \textbf{J}_{\omega}\dot{\boldsymbol{\theta}}\]

$n$-link manipulator라면 Jacobian은 $6 \times n$ matrix.

\[\textbf{J}(\boldsymbol{\theta}) = \begin{bmatrix} \textbf{J}_{v1} & \textbf{J}_{v2} \cdots \textbf{J}_{vn} \\ \textbf{J}_{\omega1} & \textbf{J}_{\omega2} \cdots \textbf{J}_{\omega n} \end{bmatrix}\]

그러므로 end-effector의 velocity는

\[\textbf{v}_E = \textbf{J}_{v1} \dot{\theta}_1 + \textbf{J}_{v2} \dot{\theta}_2 + \cdots + \textbf{J}_{vn} \dot{\theta}_n = \textbf{J}_v \dot{\boldsymbol{\theta}} \dot{\boldsymbol{\theta}} \\ \boldsymbol{\omega}_E = \textbf{J}_{\omega1} \dot{\theta}_1 + \textbf{J}_{\omega2} \dot{\theta}_2 + \cdots + \textbf{J}_{\omega n} \dot{\theta}_n = \textbf{J}_{\omega}\dot{\boldsymbol{\theta}} \dot{\boldsymbol{\theta}}\]

Revolute Joints

\[\textbf{v}_{Ei} = \textbf{J}_{vi} \dot{\theta}_i = \dot{\theta}_i \hat{\textbf{z}}_{i-1} \times {}^{i-1}\textbf{r}_E \\ \textbf{J}_{vi} = \hat{\textbf{z}}_{i-1} \times {}^{i-1}\textbf{r}_E\] \[\boldsymbol{\omega}_{Ei} = \textbf{J}_{\omega i} \dot{\theta}_1 = \dot{\theta}_i \hat{\textbf{z}}_{i-1} \\ \textbf{J}_{\omega i} = \hat{\textbf{z}}_{i-1}\] \[\textbf{J}_{i} = \begin{bmatrix} \textbf{J}_{vi} \\ \textbf{J}_{\omega i} \end{bmatrix} = \begin{bmatrix} \hat{\textbf{z}}_{i-1} \times {}^{i-1}\textbf{r}_E \\ \hat{\textbf{z}}_{i-1} \end{bmatrix}\]

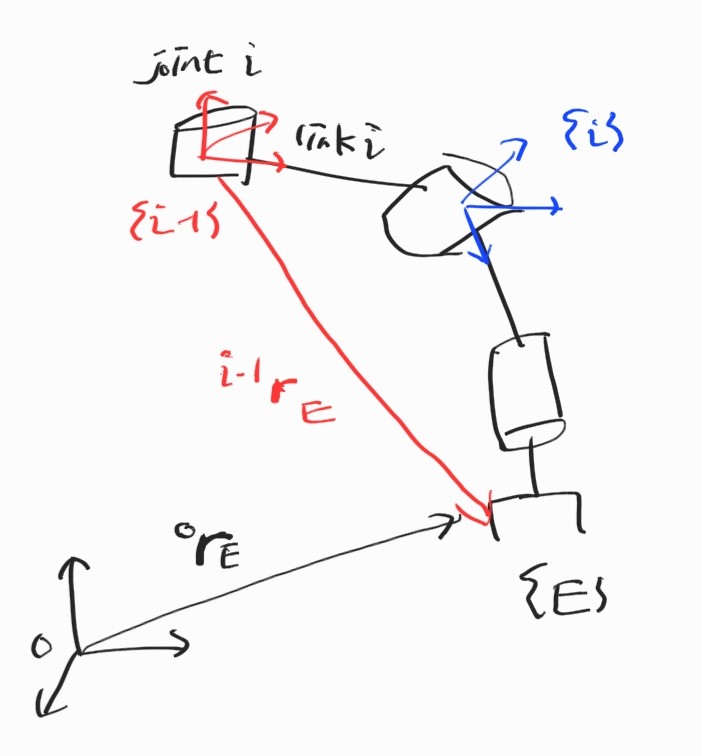
Prismatic Joints

$i$가 prismatic joint이면 rotational motion을 만들어내지 않으므로,

\[\textbf{v}_{Ei} = \textbf{J}_{vi} \dot{\theta}_i = \hat{\textbf{z}}_{i-1} \dot{d}_i \\ \textbf{J}_{vi} = \hat{\textbf{z}}_{i-1}\] \[\boldsymbol{\omega}_{Ei} = \textbf{J}_{\omega i} \dot{\theta}_1 = \textbf{0} \\ \textbf{J}_{\omega i} = \textbf{0}\] \[\textbf{J}_{i} = \begin{bmatrix} \textbf{J}_{vi} \\ \textbf{J}_{\omega i} \end{bmatrix} = \begin{bmatrix} \hat{\textbf{z}}_{i-1} \\ \textbf{0} \end{bmatrix}\]

Vector of Origin

$\{i-1 \}$ frame의 origin에서 $\{E \}$의 origin의 vector를 구하고자 한다면

\[\begin{align*} \begin{bmatrix} {}^{i-1}\textbf{r}_E \\ 1 \end{bmatrix} &= \begin{bmatrix} {}^{0}\textbf{r}_E - {}^{0}\textbf{r}_{i-1} \\ 1 \end{bmatrix} \\ \\ &= {}^{0}\textbf{T}_1(\theta_1){}^{1}\textbf{T}_2(\theta_2) \cdots {}^{n-1}\textbf{T}_n(\theta_n) \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} - {}^{0}\textbf{T}_1(\theta_1){}^{1}\textbf{T}_2(\theta_2) \cdots {}^{i-2}\textbf{T}_{i-1}(\theta_{i-1}) \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} \end{align*}\]

---

3.3.4 Completion

이제 3R planar manipulator의 Jacobian.

\[\textbf{J}(\textbf{q}) = \begin{bmatrix} \hat{\textbf{z}}_0 \times (\textbf{p}_3 - \textbf{p}_0) & \hat{\textbf{z}}_1 \times (\textbf{p}_3 - \textbf{p}_1) & \hat{\textbf{z}}_2 \times (\textbf{p}_3 - \textbf{p}_2) \\ \hat{\textbf{z}}_0 & \hat{\textbf{z}}_1 & \hat{\textbf{z}}_2 \end{bmatrix}\]

Forward kinematics로부터,

\[\textbf{p}_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}, \quad \textbf{p}_1 = \begin{bmatrix} l_1c_1 \\ l_1s_1 \\ 0 \end{bmatrix}, \quad \textbf{p}_2 = \begin{bmatrix} l_1c_1 + l_2c_{12} \\ l_1s_1 + l_2s_{12} \\ 0 \end{bmatrix}, \quad \textbf{p}_3 = \begin{bmatrix} l_1c_1 + l_2c_{12} + l_3c_{123} \\ l_1s_1 + l_2s_{12} +l_3s_{123} \\ 0 \end{bmatrix}\]

Revoulte joint axis는 planar이므로

\[\hat{\textbf{z}}_0 = \hat{\textbf{z}}_1 = \hat{\textbf{z}}_2 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]

따라서 Jacobian은 다음 형태이다.

\[\textbf{J}(\textbf{q}) = \begin{bmatrix} -l_1s_1 - l_2s_{12} -l_3s_{123} & -l_1s_1 - l_2s_{12} & -l_3s_{123} \\ l_1c_1 + l_2c_{12} + l_3c_{123} & l_1c_1 + l_2c_{12} & l_1c_1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix}\]

이를 토대로,

\[\boldsymbol{\nu} = \textbf{J}(\dot{\boldsymbol{\theta}})\]

만약 Jacobian이 singular가 아니라면,

\[\dot{\textbf{q}} = \textbf{J}^{-1}\boldsymbol{\nu}\]