1.7 Pose in 3D

---

1.7.1 Homogeneous Transformation Matrix

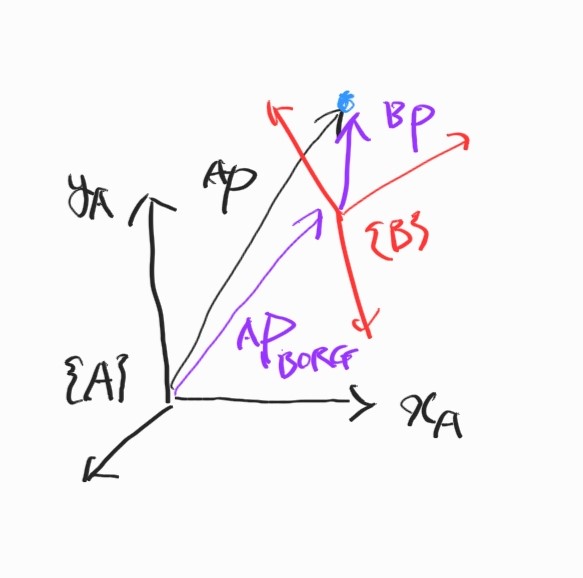
2D와 다른 점은 $z$-성분이 추가되었다는 것.

${}^A \textbf{P}_{BORG}$를 frame $\{A \}$에서 측정한 $\{B \}$의 원점의 좌표벡터라고 하자. 또, $\textbf{R}$를 $\{A \}$에 대한 $\{B \}$의 $3 \times 3$의 orthonormal matrix라고 하자.

\[{}^A \textbf{p} = {}^A \textbf{P}_{BORG} + {}^A \textbf{R}_B {}^B \textbf{p} \tag{ $ 1 $ }\] \[\begin{bmatrix} {}^Ax \\ {}^Ay \\ {}^Az \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{bmatrix} \begin{bmatrix} {}^Bx \\ {}^By \\ {}^Bz \end{bmatrix} + \begin{bmatrix} {}^A x_{BORG} \\ {}^A y_{BORG} \\ {}^A z_{BORG} \end{bmatrix}\]

하나의 행렬곱으로 표현하면

\[\begin{bmatrix} {}^Ax \\ {}^Ay \\ {}^Az \\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & {}^A x_{BORG} \\ r_{21} & r_{22} & r_{23} & {}^A y_{BORG} \\ r_{31} & r_{32} & r_{33} & {}^A z_{BORG} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} {}^Bx \\ {}^By \\ {}^Bz \\ 1 \end{bmatrix}\]

이때 좌변의 $4 \times 1$ 벡터를 homogeneous vector ${}^A \tilde{\textbf{p}}$로 나타낸다.

\[{}^A \tilde{\textbf{p}} = \begin{bmatrix} {}^A \textbf{R}_B & {}^A \textbf{P}_{BORG} \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix} {}^B \tilde{\textbf{p}}\]

중앙에 나타나는 행렬이 바로 homogeneous transform ${}^A \textbf{T}_B$.

\[{}^A \tilde{\textbf{p}} = {}^A \textbf{T}_B {}^B \tilde{\textbf{p}}\]

이로써 마침내 3D 상에서 상대적인 pose를 $4 \times 4$ matrix로 기술할 수 있게 되었다.

Ch. 1 앞부분에서 징하게 써 왔던 ${}^{A}\xi_{B}$의 의미가 드러났다. 2D의 경우는 Sec 1.2를 참조.

 (1) Pose는 Matrix다.

\[{}^{A}\xi_{B} \mapsto {}^{A} \textbf{T}_{B} = \begin{bmatrix} {}^A \textbf{R}_B & {}^A \textbf{P}_{BORG} \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix}\]

 (2) Compounding은 matrix product이다.

\[{}^{X}\xi_{Y}{}^{Y}\xi_{Z} \mapsto {}^X \textbf{T}_Y{}^Y \textbf{T}_Z\]

 (3) Negation은 matrix inverse이다.

\[-{}^{X}\xi_{Y} \mapsto \textbf{T}^{-1}\]

 (4) Vector transformation은 matrix-vector product이다.

\[\xi \textbf{p} \mapsto \textbf{T}\tilde{\textbf{p}}\]

따라서 마찬가지로, homogeneous transformation은 special Euclidean group에 속한다.

\[\textbf{T} \in SE(3)\]

---

1.7.2 Multiplication and Inverse

이 녀석들은 조금 더 구체적인 식이 있으면 편할 것 같다.

\[\textbf{T}_1 \textbf{T}_2 = \begin{bmatrix} \textbf{R}_1 & \textbf{t}_1 \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix} \begin{bmatrix} \textbf{R}_2 & \textbf{t}_2 \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix} = \begin{bmatrix} \textbf{R}_1\textbf{R}_2 & \textbf{t}_1 + \textbf{R}_1 \textbf{t}_2 \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix}\]

Inverse는 조금 계산할 여지가 있다. 직관적으로 생각하면 ${}^B \textbf{T}_A = {}^A \textbf{T}_B^{-1}$인데…

식 $(1)$의 $A$와 $B$를 바꾸면,

\[{}^B \textbf{p} = {}^B \textbf{P}_{AORG} + {}^B \textbf{R}_A {}^A \textbf{p}\]

즉, ${}^B \textbf{P}_{AORG}$와 ${}^B \textbf{R}_A$를 알아야 할 필요가 있다. 다시 식 $(1)$로 돌아가서 정리하면,

\[\begin{align*} {}^A \textbf{p} &= {}^A \textbf{P}_{BORG} + {}^A \textbf{R}_B {}^B \textbf{p} \\ \\ {}^B \textbf{p} &= -({}^A \textbf{R}_B)^{-1}{}^A \textbf{P}_{BORG} + ({}^A \textbf{R}_B)^{-1}{}^A \textbf{p} \\ &= -{}^A \textbf{R}_B^T {}^A \textbf{P}_{BORG} + {}^A \textbf{R}_B^T{}^A \textbf{p} \end{align*}\]

이므로,

\[{}^B \textbf{p} = \begin{bmatrix} {}^A \textbf{R}_B^T & -{}^A \textbf{R}_B^T {}^A \textbf{P}_{BORG} \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix}\]

이다.

따라서 간단히 표현하면,

\[\textbf{T}^{-1} = \begin{bmatrix} \textbf{R} & \textbf{t} \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix} = \begin{bmatrix} \textbf{R}^T & -\textbf{R}^T \textbf{t} \\ \textbf{0}_{1 \times 3} & 1 \\ \end{bmatrix}\]