younghwanjoo1608

ㅎㅇ

3 minute read


지금까지 rotation representation의 세 종류를 알아보았다.

  1. Rotation matrix
  2. Euler angle
  3. Quaternion

이들 사이에 어떤 관련이 있을까?

1.6.1 Quaternion vs Rotation Matrix


Quaternion $q = (q_0, \textbf{q})$으로 주어진 rotation matrix는

\[\textbf{R} = \begin{bmatrix} 1-2(q_2^2 + q_3^2) & 2(q_1q_2 - q_0q_3) & 2(q_0q_2 + q_1q_3) \\ 2(q_0q_3 + q_1q_2) & 1-2(q_1^2 + q_3^2) & 2(q_2q_3 - q_0q_1) \\ 2(q_1q_3 - q_0q_2) & 2(q_0q_1 + q_2q_3) & 1-2(q_1^2 + q_2^2) \\ \end{bmatrix}\]

이로부터 역산하면

\[q = \begin{bmatrix} \frac{1}{2} \sqrt{1+r_{11} + r_{22} + r_{33}} \\ \frac{1}{4q_0} (r_{32}-r_{23}) \\ \frac{1}{4q_0} (r_{13}-r_{31}) \\ \frac{1}{4q_0} (r_{21}-r_{12}) \\ \end{bmatrix}\]

또는,

\[q = \begin{bmatrix} \frac{1}{2} \sqrt{1+r_{11} + r_{22} + r_{33}} \\ \frac{1}{2} \textrm{sgn}(r_{32}-r_{23}) \sqrt{r_{11} - r_{22} - r_{33} +1}\\ \frac{1}{2} \textrm{sgn}(r_{13}-r_{31}) \sqrt{r_{22} - r_{33} - r_{11} +1}\\ \frac{1}{2} \textrm{sgn}(r_{21}-r_{12}) \sqrt{r_{33} - r_{11} - r_{22} +1}\\ \end{bmatrix}\]

가 된다.1

이때, $r_{ij}$는 $\textbf{R}$의 $i$행 $j$열 성분.


Composition of Rotations


Quaternion의 product 이용.

\[{}^aq_c = {}^aq_b {}^bq_c\]


Example 1


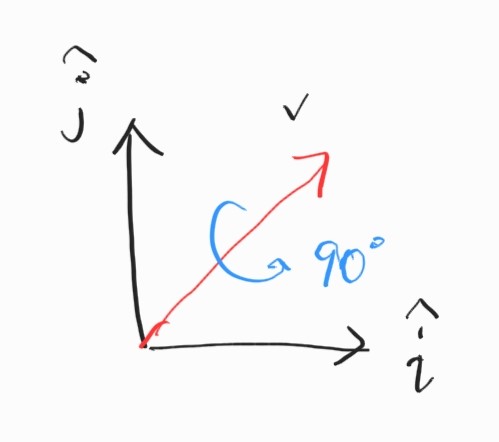
\[\textbf{v} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \end{bmatrix}\]


벡터 $\textbf{v}$를 따라 $90^{\circ}$ 회전한 quaternian을 찾아보자.

\[q = \begin{bmatrix} \cos(\frac{90^{\circ}}{2}) \\ v_1 \sin(\frac{90^{\circ}}{2}) \\ v_2 \sin(\frac{90^{\circ}}{2}) \\ v_3 \sin(\frac{90^{\circ}}{2}) \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{2} \\ \frac{1}{2} \\ 0 \\ \end{bmatrix}\]


비슷하게, $(1,0,0)$에 대해 $60^{\circ}$만큼의 회전을 나타내는 quaternion은

\[q = (\cos(\frac{60^{\circ}}{2}),sin(\frac{90^{\circ}}{2})(1,0,0)) = (0.866,0.5,0,0)\]

$q$의 conjugate와 inverse는

\[q^{\ast} = q^{-1} = (0.866,-0.5,0,0)\]


일반적으로, $x$-, $y$-, $z$-축에 대한 임의의 rotation을 나타내는 quaternion은

Rotation about $x$ : $q = (\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2}), 0, 0)$

Rotation about $y$ : $q = (\cos(\frac{\theta}{2}),0, \sin(\frac{\theta}{2}), 0)$

Rotation about $z$ : $q = (\cos(\frac{\theta}{2}),0, 0, \sin(\frac{\theta}{2}))$


Example 2


점 $\textbf{p} = \begin{bmatrix} 3 & 5 & 2 \end{bmatrix}^T$를 축 $\begin{bmatrix} 1 & 0 & 0 \end{bmatrix}^T$를 기준으로 $60^{\circ}$ 회전한 결과를 구하라.


Using quaternion.


\[\begin{align*} p &= (0,3,5,2) \\ \\ p_{rot} &= q(0,3,5,2)q^{\ast} \\ &= (0.866, 0.5, 0, 0)(0, 3,5,2)(0.866, -0.5, 0, 0) \\ &= (-1.5, 2.6, 3.33, 4.23)(0.866, 0.5, 0, 0) \\ &= (0, 3, 0.768, 5.33) &\Rightarrow \textbf{p}_{rot} = \begin{bmatrix} 3 & 0.768 & 5.33 \end{bmatrix}^T \end{align*}\]

$\square$


Using rotation matrix.


\[\textbf{p}_{rot} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos 60^{\circ} & -\sin 60^{\circ} \\ 0 & \sin 60^{\circ} & \cos 60^{\circ} \\ \end{bmatrix} \begin{bmatrix} 3 \\ 5 \\ 2 \end{bmatrix} = \begin{bmatrix} 3 \\ 0.768 \\ 5.33 \end{bmatrix}\]

$\square$


Example 3


다음 rotation matrix와 동치인 unit quaternion을 구하라.

\[\textbf{R} = \begin{bmatrix} -\frac{1}{2} & 0 & -\frac{\sqrt{3}}{2} \\ 0 & 1 & 0 \\ \frac{\sqrt{3}}{2} & 0 & -\frac{1}{2} \\ \end{bmatrix}\]


Ans.


\[q_0 = \frac{1}{2} \sqrt{1+r_{11} + r_{22} + r_{33}} = \frac{1}{2} \sqrt{1-\frac{1}{2} + 1 -\frac{1}{2}} = \frac{1}{2} \\ q_x = \frac{1}{4q_0} (r_{32}-r_{23}) = 0 \\ q_y = \frac{1}{4q_0} (r_{13}-r_{31}) = -\frac{\sqrt{3}}{2} \\ q_z = \frac{1}{4q_0} (r_{21}-r_{12}) = 0\\\]

그러므로 quaternion은

\[q = (q_0, \textbf{q}) = (\frac{1}{2} , 0,-\frac{\sqrt{3}}{2}, 0 )\]

$\square$


Robotics Toolbox - Quaternion


UnitQuaternion 함수는 rotation matrix를 unit quaternion으로 바꾸어 준다.

R = rpy2tr(0.1, 0.2, 0.3)
q = UnitQuaternion(R)

 q =

   0.98335 < 0.034271, 0.10602, 0.14357 >


q.plot()




inv(q)

 ans =

   0.98335 < -0.034271, -0.10602, -0.14357 >

q * inv(q)

 ans =

   1 < 0, 0, 0 >

q/q

 ans =

   1 < 0, 0, 0 >


다시 quaternion을 orthonormal rotation matrix로 만들려면,

q.R

 ans =

   0.9363  -0.2751  0.2184

   0.2896  0.9564  -0.0370

   -0.1987  0.0978  0.9752


1.6.2 Quaternion vs Euler Angles

다시 quaternion $q$로부터 만든 rotation matrix $\textbf{R}$는

\[\textbf{R} = \begin{bmatrix} 1-2(q_2^2 + q_3^2) & 2(q_1q_2 - q_0q_3) & 2(q_0q_2 + q_1q_3) \\ 2(q_0q_3 + q_1q_2) & 1-2(q_1^2 + q_3^2) & 2(q_2q_3 - q_0q_1) \\ 2(q_0q_2 + q_1q_3) & 2(q_0q_1 + q_2q_3) & 1-2(q_1^2 + q_2^2) \\ \end{bmatrix}\]

$Z-Y-X$ Euler angle의 경우, 각 $\alpha$, $\beta$, $\gamma$는 다음과 같이 결정된다.2

\[\begin{align*} \beta &= \arctan(-r_{31}, \sqrt{r_{11}^2 + r_{21}^2}) \\ \alpha &= \arctan(\frac{r_{21}}{c \beta}, \frac{r_{11}}{c \beta}) \\ \gamma &= \arctan(\frac{r_{32}}{c \beta}, \frac{r_{33}}{c \beta}) \\ \end{align*}\]


$ZYX$ Euler angle 역시 quaternion으로 다음과 같이 표현 가능.

\[q(\hat{\textbf{z}}, \alpha) = \begin{bmatrix} \cos(\frac{\alpha}{2}) \\ 0 \\ 0 \\ \sin(\frac{\alpha}{2}) \end{bmatrix} \qquad q(\hat{\textbf{y}}, \beta) = \begin{bmatrix} \cos(\frac{\alpha}{2}) \\ 0 \\ \sin(\frac{\alpha}{2}) \\ 0 \end{bmatrix} \qquad q(\hat{\textbf{z}}, \gamma) = \begin{bmatrix} \cos(\frac{\alpha}{2}) \\ \sin(\frac{\alpha}{2}) \\ 0 \\ 0 \end{bmatrix}\]

따라서 $ZYX$ Euler angle에 대한 quaternion 역시 연속된 quaternion들의 곱으로 나타난다.

\[q = q(\hat{\textbf{z}}, \alpha)q(\hat{\textbf{y}}, \beta)q(\hat{\textbf{z}}, \gamma)\]


1.6.3 Comparison


Format # of parameters Singularity? Compounding
Rotation Matrix 9 No Matrix Multiplication
Euler angles/rpy 3 Yes Non-trivial
Angle + axis 3(1+2) No, but problem for zero rotation Non-trivial
Quaternion 4 No Quaternion multiplication


  1. 후자의 경우가 numerically stable. ↩

  2. MATLAB에서는 `atan2` 함수를 사용. ↩

You may also enjoy