1.5 Quaternion
1.5.1 Complex Number
복소수 $\textbf{z}$는 복소평면 위의 한 vector이다.
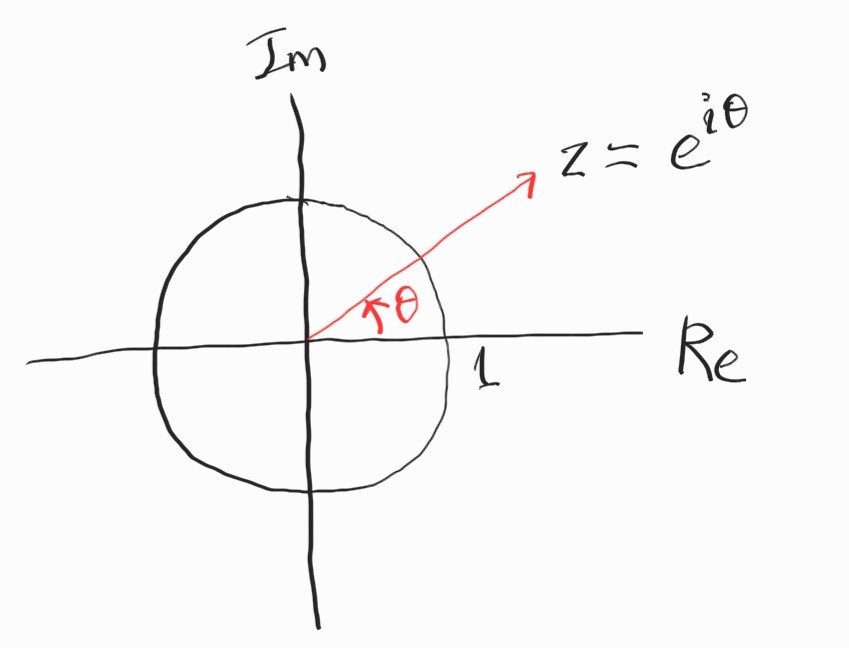
Euler’s formula $e^{i \theta} = \cos \theta + i \sin \theta$를 이용하면, 임의의 복소수는 다음과 같이 나타낼 수 있다.
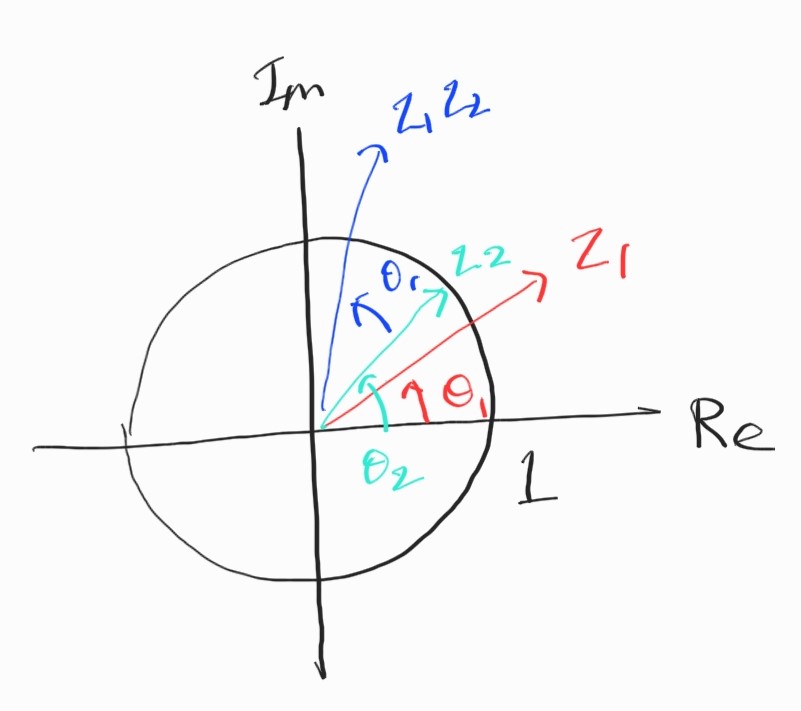
\[\textbf{z} = | \textbf{z} |e^{i \theta} = re^{i \theta}\]$\textbf{z}_1$, $\textbf{z}_2$가 복소수이며, $\vert \textbf{z}_2 \vert = 1$이라고 하자.
복소수 $\textbf{z}$는 복소평면 위의 한 벡터이므로, 곱 $\textbf{z}_1 \textbf{z}_2$는 벡터 $\textbf{z}_1$을 평면 위에서 각도 $\theta_2$만큼 회전시킨 것과 같다.
1.5.2 Rotation on Plane
2D vector $\textbf{v}$를 각도 $\alpha$만큼 회전시키자.
임의의 벡터 $\textbf{v} = (a,b)$에 대해 $\textbf{v}$를 복소수 $\textbf{v} = a+ib = \vert \textbf{v} \vert (\cos \theta + i \sin \theta)$로 생각할 수 있다.
임의의 단위 복소벡터 $\textbf{R} = \cos \alpha + i \sin \alpha$에 대해 $\textbf{R}$과 $\textbf{v}$를 곱하면 회전한 복소벡터를 얻게 된다.
\[\textbf{v}' = \textbf{R}\textbf{v} = \vert \textbf{v} \vert e^{i(\theta + \alpha)}\]위와 같은 방법으로, 회전된 평면 상의 2D vector $\textbf{v}’$을 다음과 쓸 수 있다.
\[\begin{align*} \textbf{v}' &= (a+ib)(\cos \alpha + i \sin \alpha) \\ &= (a \cos \alpha - b \sin\alpha) + i(a \sin \alpha + b \cos \alpha) \end{align*}\]위 식을 matrix form으로 바꾸면,
\[\textbf{v}' = \begin{bmatrix} a \cos \alpha - b \sin\alpha & a \sin \alpha + b \cos \alpha \\ \end{bmatrix}^T\] \[\begin{bmatrix} a' \\ b' \end{bmatrix} = \begin{bmatrix} \cos \alpha & -\sin\alpha \\ \sin\alpha & \cos \alpha \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix}\]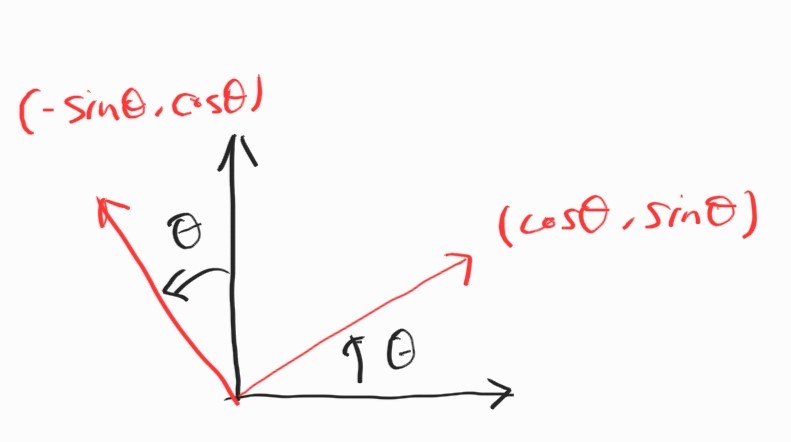
1.5.3 Quaternion
W. R. Hamiltion은 복소수들의 algebra와 rotation on plane 사이의 관계를 연구하고, 3D space에서의 관계를 유추해 quaternion을 발견하였다.
Hyper complex number는 scalar와 vector의 합으로 표현된다.
\[q = q_0 + q_1\textbf{i} + q_2\textbf{j} + q_3\textbf{k} = q_0 + \textbf{q} = \begin{bmatrix} q_0 \\ \textbf{q} \end{bmatrix}\]여기서 $q_0$는 scalar part, $\textbf{q}$는 $\mathbb{R}^3$ 상의 ordinary vector. $\textbf{i}$, $\textbf{j}$, $\textbf{k}$는 $\mathbb{R}^3$의 standard orthonormal basis이다.
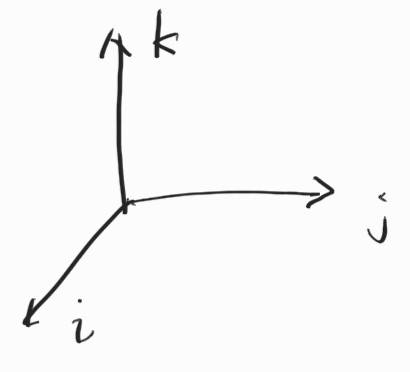
이로써 3D 상에서 복소수의 일반화가 완성.
\[q = q_0 + iq_1 + jq_2 + kq_3 = (q_0, q_1, q_2, q_3) \\ i^2 = j^2 = k^2 = ijk = -1\]1.5.4 Multiplication
간단한 성질의 증명은 생략하자. 예를 들어
- 두 quatertion이 같다는 건 각 성분이 같다는 것과 동치
- Quaternion의 set은 addition에 대해 닫혀 있다
- zero quaternion $(0,0,0,0)$이 존재
- 각 quaternion $q$에는 negative $-q$가 존재.
- 덧셈은 commutative & associative
곱셈부터 시작. Scalar $c$에 대해
\[cq = cq_0 + icq_1 + jcq_2 + kcq_3 = (cq_0, cq_1, cq_2, cq_3)\]몇 가지 special product를 기억해 둘 것.
\[i^2 = j^2 = k^2 = ijk = -1 \\ ij = k = -ji \\ jk = i = -kj \\ ki = j = -ik\]두 quaternion 사이의 곱
\[p = p_0 + ip_1 + jp_2 + kp_3 \qquad q = q_0 + iq_1 + jq_2 + kq_3 \\ pq = (p_0 + ip_1 + jp_2 + kp_3)(q_0 + iq_1 + jq_2 + kq_3)\]각 성분끼리 묶으면,
\[\begin{align*} pq &= p_0q_0 - (p_1q_1 + p_2q_2 + p_3q_3) + p_0(iq_1 + jq_2 + kq_3) + q_0(ip_1 + jp_2 + kp_3) \\ &+ i(p_2q_3 - p_3q_2) + j(p_3q_1 - p_1q_3) + k(p_1q_2 - p_2q_1) \end{align*}\]따라서,
\[pq = p_0q_0 - \textbf{p}\cdot \textbf{q} + p_0 \textbf{q} + q_0 \textbf{p} + \textbf{p} \times \textbf{q}\]Cross product 항이 있는 것에 주목. 이로 인해 commutative가 성립하지 않는다!
\[pq \not= qp\]1.5.5 Complex Conjugate
Quaternion $q$가
\[q = q_0 + \textbf{q} = q_0 + iq_1 + jq_2 + kq_3\]이면, $q$의 compex conjugate는
\[q^{\ast} = q_0 - \textbf{q} = q_0 - iq_1 - jq_2 - kq_3\]그러므로,
\[q + q^{\ast} = 2q_0 \\ (pq)^{\ast} = q^{\ast}p^{\ast}\]1.5.6 Norm
\[N(q) = \vert q \vert = \sqrt{q^{\ast}q}\]그러므로,
\[\begin{align*} N^2(q) &= q^{\ast}q = (q_0, -\textbf{q})(q_0, +\textbf{q}) \\ &= q_0q_0 - (-\textbf{q}) \cdot \textbf{q} + q_0 \textbf{q} + q_0(-\textbf{q}) + (-\textbf{q}) \times \textbf{q} \\ &= q_0q_0 + \textbf{q} \cdot \textbf{q} \\ &= q_0^2 + q_1^2 + q_2^2 + q_3^2 \\ &= \vert q \vert^2 \end{align*}\]이 연산 결과는 복소수와 유사하다.
\[(a-ib)(a+ib) = a^2 -(ib)^2 = a^2 + b^2\]그럼 두 quaternion $p$, $q$의 곱의 norm을 구해보자. 결과는 각 norm의 곱과 같다.
\[\begin{align*} N^2(pq) &= (pq)^{\ast}(pq) \\ &= q^{\ast}p^{\ast}pq \\ &= q^{\ast} N^2(p)q \\ &= N^2(p)q^{\ast}q \\ &= N^2(p)N^2(q) \end{align*}\] \[\begin{align*} N(pq) &= \sqrt{N^2(p)N^2(q)} \\ &= \sqrt{N^2(p)}\sqrt{N^2(q)} \\ &= N(p)N(q) \end{align*}\]1.5.7 Inverse of Quaternion
모든 non-zero quaternion $q$는 muliplicative inverse $q^{-1}$를 갖는다.
\[q^{-1}q = qq^{-1} = 1\]앞뒤로 $q^{\ast}$를 곱하면,
\[q^{-1}qq^{\ast} = q^{\ast}qq^{-1} = q^{\ast}\]그런데 $qq^{\ast} = N^2(q)$이므로,
\[q^{-1} = \frac{q^{\ast}}{N^2(q)} = \frac{q^{\ast}}{\vert q \vert^2}\]이것으로 quaternion의 기본 연산 성질은 끝!
1.5.8 Pure Quaternion
이제 드디어 quaternion과 rotation 사이의 관계.
$\mathbb{R}^3$ 상의 rotation은 $3 \times 3$의 행렬 형태로 나타나며, 그 determinant는 $+1$이다. Quaternion이 이 rotation operator의 alternative form이 된다.
어라, quaternion은 $\mathbb{R}^4$에 있는데 $\mathbb{R}^3$ 상의 vector를 어떻게 다루지?
벡터 $\textbf{v} \in \mathbb{R}^3$를 scalar part가 zero인 quaternion $q \in \mathbb{R}^4$로 생각하자! 이러한 quaternion을 pure quaternion이라고 한다.
따라서, pure quaternion의 set $Q_0$는 모든 quaternion의 set $Q$의 subset. $\mathbb{R}^3$와 $Q_0$ 사이에는 one-to-one mapping이 존재.
\[\textbf{v} \in \mathbb{R}^3 \leftrightarrow (v = 0+\textbf{v}) \in Q_0 \subset Q\]이제 $qv$가 벡터 $\textbf{v}$를 어떻게 회전시키는지 확인하자.
\[\begin{align*} qv &= (q_0 + \textbf{q})(0 + \textbf{v}) \\ &= -\textbf{q} \cdot \textbf{v} + q_0 \textbf{v} + \textbf{q} \times \textbf{v} \end{align*}\]계산 결과가 pure quaternion이려면, $\textbf{q} \cdot \textbf{v}=0$이어야만 한다. $\mathbb{R}^3$ 상의 vector rotation을 다루는 다른 방식의 곱셈이 있을 것 같은데…
다음 product는 계산 결과가 quaternion $w \in Q_0$이 됨을 보장한다.
\[qvq^{\ast} \qquad \textrm{and} \qquad q^{\ast}vq\]1.5.9 Unit Quaternion
Rotation $\vert \textbf{q} \vert = 1$을 생각하자.
Euler’s Rotation Theorem(1.3.2)과 Rodrigues’ Formula(Sec 1.4)를 상기. $\mathbb{R}^3$ 상의 임의의 rotation은 어떤 축 $\textbf{n}$에 다한 각도 $\theta$만큼의 회전으로 표현할 수 있다!
Unit quaternion을 unit axis $\hat{\textbf{k}}$에 대한 각도 $\theta$만큼의 회전으로 쓰면,
\[q=(q_0, \textbf{q}) = \left( \cos \frac{\theta}{2}, \hat{\textbf{k}} \sin \frac{\theta}{2} \right)\]이다.
Proof.
왜 $\theta$가 아니라 $\frac{\theta}{2}$일까?
Unit quaternion $\textbf{u} = \cos \theta + i \sin \theta$라고 하자.
pure quaternion $j$에 대해 product $\textbf{u}j\textbf{u}^{\ast}$를 계산하면
\[\begin{align*} (\cos \theta + i \sin \theta)j(\cos \theta - i \sin \theta) &= (\cos \theta + i \sin \theta)(j\cos \theta +k \sin \theta) \\ &= (\cos^2 \theta - \sin^2 \theta)j + 2k(\cos \theta \sin \theta) \\ &= j \cos 2\theta + k \sin 2\theta \end{align*}\]즉, vector $\textbf{j}$를 회전축 $\textbf{i}$에 대해 각도 $2 \theta$만큼 회전시킨 결과와 같다. 그래서 $\theta$가 아니라 $\frac{\theta}{2}$를 사용하는 것. $\square$
따라서, 3D rotation을 다음과 같이 해석할 수 있다.
\[q_0 = \cos \frac{\theta}{2} \qquad \textbf{q} = \hat{\textbf{k}} \sin \frac{\theta}{2}\]1.5.10 Application to Rotation
이제 계산만 남았다.
Vector $\textbf{r}$의 회전 $q$를 계산하는 절차는 다음과 같다.
(1) 벡터 $\textbf{v}$를 quaternion으로 변환.1
\[v = (0, \textbf{v})\](2) Rotation $q$를 적용.
\[v_{qrot} = qvq^{\ast}\](3) 회전된 벡터는 다음 quaternion의 성분이 된다.
\[v_{qrot} = (0,\textbf{v}_{rot})\]Vector formula
\[\begin{align*} v_{qrot} &= qvq^{\ast} \\ \\ vq^{\ast} &= (0, \textbf{v})(q_0, -\textbf{q}) = (\textbf{v} \cdot \textbf{q}, q_0 \textbf{v} - \textbf{v} \times \textbf{q}) \\ \\ qvq^{\ast} &= (q_0, \textbf{q})(\textbf{v} \cdot \textbf{q}, q_0 \textbf{v} - \textbf{v} \times \textbf{q}) \\ &= (0, \textbf{v} + 2q_0 \textbf{q} \times \textbf{v} + 2 \textbf{q} \times (\textbf{q} \times \textbf{v})) \end{align*}\]Matrix formula
먼저 일반적인 quaternion product부터.
\[pq = p_0q_0 - \textbf{p}\cdot \textbf{q} + p_0 \textbf{q} + q_0 \textbf{p} + \textbf{p} \times \textbf{q}\]$p$를 quaternion matrix $P$로 표현하고자 한다.
\[P = \begin{bmatrix} p_0 & -p_1 & -p_2 & -p_3 \\ p_1 & p_0 & -p_3 & p_2 \\ p_2 & p_3 & p_0 & -p_1 \\ p_3 & -p_2 & p_1 & p_0 \\ \end{bmatrix} = \begin{bmatrix} p_0 & -\textbf{p}^T \\ \textbf{p} & p_0 \textbf{I} + [\textbf{p}]_{\times} \\ \end{bmatrix}\] \[Pq = \begin{bmatrix} p_0 & -p_1 & -p_2 & -p_3 \\ p_1 & p_0 & 0 & 0 \\ p_2 & 0 & p_0 & 0 \\ p_3 & 0 & 0 & p_0 \\ \end{bmatrix} \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -p_3 & p_2 \\ 0 & p_3 & 0 & -p_1 \\ 0 & -p_2 & p_1 & 0 \\ \end{bmatrix} \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix} = \begin{bmatrix} p_0 & -\textbf{p}^T \\ \textbf{p} & p_0 \textbf{I} + [\textbf{p}]_{\times} \\ \end{bmatrix} \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix}\]유사하게, $pq^{\ast}$는
\[\begin{align*} pq^{\ast} &= p_0q_0 + \textbf{p}\cdot \textbf{q} - p_0 \textbf{q} + q_0 \textbf{p} - \textbf{p} \times \textbf{q} \\ \\ &= \begin{bmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \\ \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \\ \end{bmatrix} \end{align*}\]그러므로, $qpq^{\ast}$는
\[\begin{align*} qpq^{\ast} &= \begin{bmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \\ \end{bmatrix} \begin{bmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \\ \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \\ \end{bmatrix} \\ \\ &= \begin{bmatrix} q_0^2 + q_1^2 + q_2^2 + q_3^2 & 0 & 0 & 0 \\ 0 & q_0^2 + q_1^2 - q_2^2 - q_3^2 & 2(q_1q_2 - q_0q_3) & 2(q_0q_2 + q_1q_3) \\ 0 & 2(q_0q_3 + q_1q_2) & q_0^2 - q_1^2 + q_2^2 - q_3^2 & 2(q_2q_3 - q_0q_1) \\ 0 & 2(q_0q_2 + q_1q_3) & 2(q_0q_1 + q_2q_3) & q_0^2 - q_1^2 - q_2^2 + q_3^2 \\ \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \\ \end{bmatrix} \end{align*}\]Quaternion의 성질
\[q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1 \\ q_0^2 + q_1^2 - q_2^2 - q_3^2 = 1-2(q_2^2 + q_3^2)\]을 이용하면, rotation의 matrix form은 다음과 같다.
\[qpq^{\ast} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1-2(q_2^2 + q_3^2) & 2(q_1q_2 - q_0q_3) & 2(q_0q_2 + q_1q_3) \\ 0 & 2(q_0q_3 + q_1q_2) & 1-2(q_1^2 + q_3^2) & 2(q_2q_3 - q_0q_1) \\ 0 & 2(q_0q_2 + q_1q_3) & 2(q_0q_1 + q_2q_3) & 1-2(q_1^2 + q_2^2) \\ \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \\ \end{bmatrix}\]-
앞으로 Robotics에서는 quaternion이라고 하면 unit quaternion을 의미하기로 하자. ↩
