1.4 Rodrigues’ Formula
임의의 orientation을 갖는 두 orthonormal coordinate frame 사이의 관계는 어떤 축에 대한 단 하나의 rotation으로 표현할 수 있다!
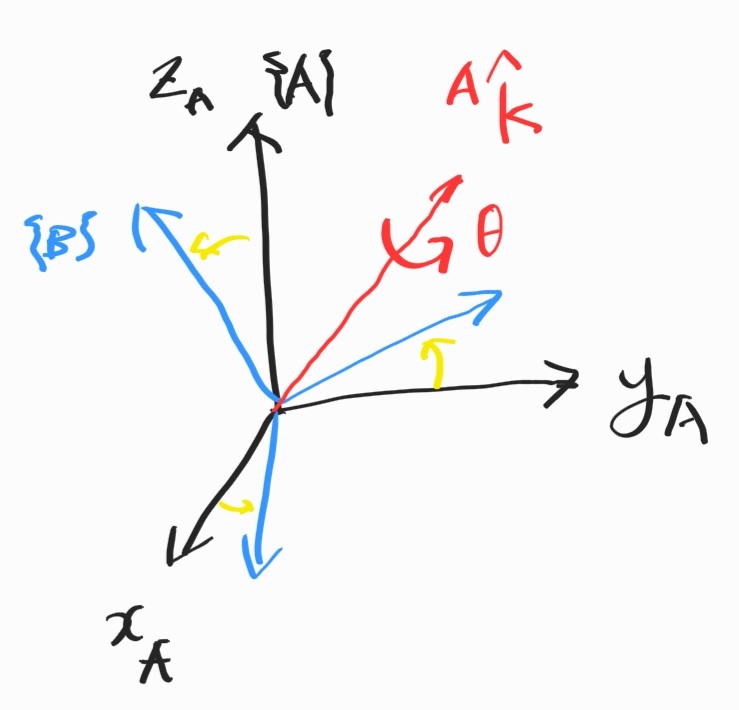
이러한 angle-axis representation은 angle axis와 angle pair로 구성된다. ${}^A \hat{\textbf{k}}$는 unit vector로, 회전 각도는 ccw가 양이라고 하자.1 이때,
\[{}^A \hat{\textbf{k}} = \begin{bmatrix} k_x & k_y & k_z \end{bmatrix}^T\]1.4.1 Rodrigues’ Formula
\[\textbf{R}(\hat{\textbf{k}}, \theta) = \hat{\textbf{k}}\hat{\textbf{k}}^T + (\textbf{I}-\hat{\textbf{k}}\hat{\textbf{k}}^T)\cos{\theta} + \begin{bmatrix} \hat{\textbf{k}} \end{bmatrix}_{\times}\sin{\theta}\]또는 다르게 표현하면,
\[\textbf{R}(\hat{\textbf{k}}, \theta) = \textbf{I}_{3 \times 3} + \sin{\theta} \begin{bmatrix} \hat{\textbf{k}} \end{bmatrix}_{\times} + (1-\cos{\theta})\begin{bmatrix} \hat{\textbf{k}} \end{bmatrix}_{\times}^2\]여기서 $\begin{bmatrix} \hat{\textbf{k}} \end{bmatrix}_{\times}$는 skew-symmetric matrix. $2 \times 2$의 경우에서 확장하면,
\[\begin{bmatrix} \omega \end{bmatrix}_{\times} = \begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_z & 0 \\ \end{bmatrix}\]이러한 행렬은 벡터의 cross product를 행렬곱 \(\textbf{v}_1 \times \textbf{v}_2 = \begin{bmatrix} v \end{bmatrix}_{\times} \textbf{v}_2\) 로 표현할 수 있게 해 준다.
Proof of Rodrigues’ Formula
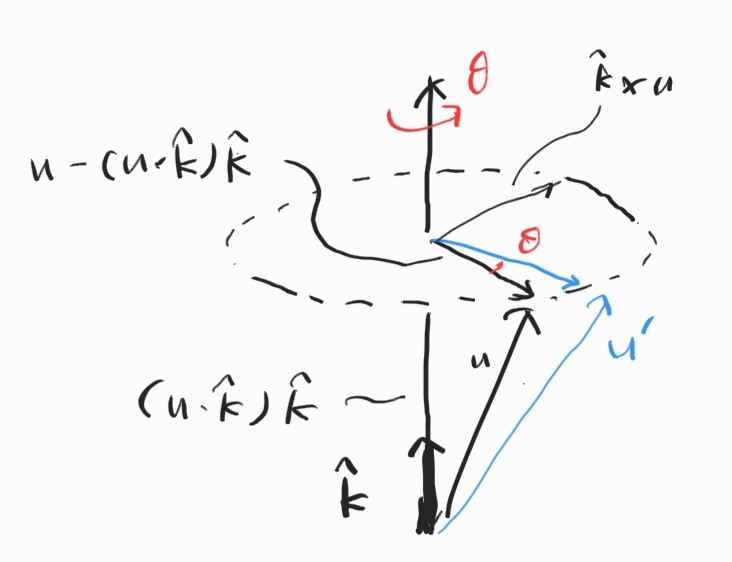
$\textbf{u}$가 우리가 회전시키고자 하는 vector라고 하자. $\textbf{u}$를 $\hat{\textbf{k}}$를 축으로 하여 각도 $\theta$만큼 회전시킨 결과를 $\textbf{u}’$라고 하자. $\textbf{u}’$를 $\textbf{u}$와 rotation matrirx로 표현하고자 한다.
$\textbf{u}$의 $\hat{\textbf{k}}$ 방향 성분은 내적을 이용해 다음과 같이 나타낼 수 있다.
\[(\textbf{u} \cdot \hat{\textbf{k}})\hat{\textbf{k}} \tag{ $ 1 $ }\]그러면 $\hat{\textbf{k}}$와 수직인 평면에서의 $\textbf{u}$의 성분은
\[\textbf{u} - (\textbf{u} \cdot \hat{\textbf{k}})\hat{\textbf{k}}\]외적에 의해 이 평면 위에서 $\textbf{u}$와 수직인 벡터는
\[\begin{align*} &\hat{\textbf{k}} \times (\textbf{u} - (\textbf{u} \cdot \hat{\textbf{k}})\hat{\textbf{k}}) \\ &= \hat{\textbf{k}} \times \textbf{u} - \hat{\textbf{k}} \times (\textbf{u} \cdot \hat{\textbf{k}})\hat{\textbf{k}} \\ &= \hat{\textbf{k}} \times \textbf{u} \end{align*}\]이제 orthogonal한 두 벡터로 평면과 평행한 $\textbf{u}’$의 성분을 구할 수 있게 되었다. 각도 $\theta$만큼 회전시킨 것과 같다는 점을 이용하면,
\[\begin{align*} \textbf{u}' &= (\textbf{u} \cdot \hat{\textbf{k}})\hat{\textbf{k}} + (\textbf{u} - (\textbf{u} \cdot \hat{\textbf{k}})\hat{\textbf{k}}) \cos{\theta} + (\hat{\textbf{k}} \times \textbf{u}) \sin{\theta} \\ &= (\hat{\textbf{k}}\hat{\textbf{k}}^T)\textbf{u} + (\textbf{I} - \hat{\textbf{k}}\hat{\textbf{k}}^T)\cos{\theta} \textbf{u} + (\hat{\textbf{k}} \times \textbf{u}) \sin{\theta} \\ &= \hat{\textbf{k}}\hat{\textbf{k}}^T\textbf{u} + (\textbf{I} - \hat{\textbf{k}}\hat{\textbf{k}}^T)\cos{\theta} \textbf{u} + \begin{bmatrix} \hat{\textbf{k}} \end{bmatrix}_{\times} \sin{\theta} \textbf{u} \end{align*}\]그러므로,
\(\textbf{R}(\hat{\textbf{k}}, \theta) = \hat{\textbf{k}}\hat{\textbf{k}}^T + (\textbf{I}-\hat{\textbf{k}}\hat{\textbf{k}}^T)\cos{\theta} + \begin{bmatrix}
\hat{\textbf{k}}
\end{bmatrix}_{\times}\sin{\theta}\)
$\square$
1.4.2 Inverse Problem
Rodrigues’ Formula $(1)$로부터 $\theta$와 $\hat{\textbf{k}}$의 값을 구하면,
\[\textbf{R}(\hat{\textbf{k}}, \theta) = \begin{bmatrix} r_11 & r_12 & r_13 \\ r_21 & r_22 & r_23 \\ r_31 & r_32 & r_33 \\ \end{bmatrix}\] \[\theta = \cos^{-1}(\frac{r_11+r_22+r_33 -1}{2})\] \[\hat{\textbf{k}} = \frac{1}{2 \sin{\theta}} \begin{bmatrix} r_32 - r_23 \\ r_13 - r_31 \\ r_21 - r_12 \\ \end{bmatrix}\]Eigenvalue, Eigenvector
Rotation이 발생하는 축은 rotation에 영향을 받지 않는다는 것을 생각하면, rotation axis는 rotation matrix $\textbf{R}$의 eigenvector이다.
\[\textbf{Rv} = \lambda \textbf{v}, \qquad \lambda = 1\]즉, rotation matrix는 eigenvalue 1에 해당되는 real eigenvector를 항상 가지게 된다.
여기에 나머지 eigenvector들을 complex value
\[\lambda \cos{\theta} \pm i \sin{\theta}\]로 나타내면, $\theta$가 바로 rotation angle이 된다.
Robotics Toolbox - Inverse Problem
예를 들어 다음 rotation을 생각.
R = rpy2r(0.1, 0.2, 0.3);
이 rotation matrix에 해당하는 회전축과 회전 각도는
[theta, v] = tr2angvec(R)
th =
0.3655
v =
0.1886 0.5834 0.7900
함수 tr2angvec로 계산된 theta는 회전 각도, v는 회전축이다.
$\textbf{R}$의 eigenvalue와 eigenvector를 구해 보자. MATLAB 내장 함수 eig를 사용.
[x, e] = eig(R)
x =
-0.6944 + 0.0000i -0.6944 + 0.0000i 0.1886 + 0.0000i
0.0792 + 0.5688i 0.0792 - 0.5688i 0.5834 + 0.0000i
0.1073 - 0.4200i 0.1073 + 0.4200i 0.7900 + 0.0000i
e =
0.9339 + 0.3574i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.9339 - 0.3574i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 + 0.0000i
이로부터 각도 정보만 뽑아내면,
theta = angle(e(1, 1))
theta =
0.3655
angvec2r 함수는 Rodrigues’ Formula로부터 직접 rotation matrix를 계산한다. 각도와 회전축 정보를 parameter로 사용한다.
R = angvec2r(pi/2, [1 0 0])
R =
1.0000 0 0
0 0.0000 -1.0000
0 1.0000 0.0000
-
${}^A \hat{\textbf{k}}$는 2 DOF, $\theta$는 1 DOF이므로 합쳐서 3 DOF. ↩
