younghwanjoo1608

ㅎㅇ

6 minute read


3D의 경우 2D에서 $z$-축이 추가된다. 방향은 right-hand rule을 따른다. 축에 평행한 단위 벡터들을 $\hat{\textbf{x}},\hat{\textbf{y}},\hat{\textbf{z}}$라고 하면,

\[\begin{align*} \hat{\textbf{z}} &= \hat{\textbf{x}} \times \hat{\textbf{y}} \\ \hat{\textbf{x}} &= \hat{\textbf{y}} \times \hat{\textbf{z}} \\ \hat{\textbf{y}} &= \hat{\textbf{z}} \times \hat{\textbf{x}} \\ \end{align*} \tag{ $ 1 $ }\]

점 $\textbf{P}$는 좌표 $(x,y,z)$ 또는 벡터

\[\textbf{p} = x\hat{\textbf{x}} + y\hat{\textbf{y}}+z\hat{\textbf{z}}\]

로 표현된다.


1.3.1 Orientation in 3D

3D에서는 더 이상 rotation이 commutative가 아니다. 이제부턴 rotation의 순서가 중요해진다.


Orthonormal Rotational Matrix

2D에서와 마찬가지다. $3 \times 3$ orthonormal matrix ${}^{A}\textbf{R}_{B}$를 이용해 frame $\{B \}$에서 표현된 벡터를 frame $\{A \}$에서 표현하려면

\[\begin{bmatrix} {}^A x \\ {}^A y \\ {}^A z \\ \end{bmatrix} = {}^A \textbf{R}_B \begin{bmatrix} {}^B x \\ {}^B y \\ {}^B z \\ \end{bmatrix}\]


Orthonormal Rotation matrix의 성질

이하 내용은 Sec. 1.2의 2D 내용과 같다.

\[{}^X \textbf{R}_Y\]

는 2D rotational matrix로 다음 성질들을 갖는다.

  1. Orthonormal. 즉, 각 column들은 unit vector이며 orthogonal이다.

  2. 각 column들은 frame $X$에 대하여 회전된 frame $Y$의 축을 정의한다.

  3. 이 matrix는 special orthogonal group에 속한다. 즉 $\textbf{R} \in SO(3) \subset \mathbb{R}^{3 \times 3}$

  4. Determinant는 $+1$이다. 따라서 변환 이후에도 벡터의 길이는 변하지 않는다. 즉, $\Vert {}^Y \textbf{p} \Vert = \Vert {}^X \textbf{p} \Vert, \forall \theta$

  5. Inverse는 transpose와 같다. 즉, $\textbf{R}^{-1} = \textbf{R}^T$


$x$-, $y$-, $z$-축에 관한 각도 $\theta$만큼의 orthonormal rotation matrix는 다음과 같다.

\[\begin{align*} R_x(\theta) &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \\ \end{bmatrix} \\ \\ R_y(\theta) &= \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \\ \end{bmatrix} \\ \\ R_z(\theta) &= \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \\ \end{align*}\]


Robotics Toolbox - Rotational Matrix

$\textbf{R}_x(\theta)$를 계산하는 함수는,

R = rotx(pi/2)

 R =

    1.0000   0   0

    0   0.0000   -1.0000

    0   1.0000   0.0000

단위가 deg인 것에 주의.1 마찬가지로 roty, rotz 함수도 존재.


그래프로 좌표계를 보고싶다면

trplot(R)



또, 직접 회전하는 모습을 볼 수도 있다.

tranimate(R)



Rotational matrix의 composition.

R = rotx(pi/2) * roty(pi/2)
S = roty(pi/2) * rotx(pi/2)

 R =

    0.0000   0   1

    1   0.0000   0.0000

    0.0000   1   0.0000

 S =

    0.0000   1   0.0000

    0   0.0000   -1

    -1   0.0000   0.0000

합성의 순서를 바꾸면 값이 달라짐을 알 수 있다.

Reading an Orthonormal Rotation Matrix

왼쪽부터 오른쪽으로 column을 읽어나가면, 새로운 frame의 축 방향을 현재 좌표계에 대해 읽을 수 있다. 예를 들어,

\[R= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 1 \\ \end{bmatrix}\]

이라고 하자. 그러면 $R$에 의해 새로 만들어지는 frame의 $x$-축은 기존의 $x$-방향 $(1,0,0)$과 같다. $y$-축은 기존의 $(0,0,1)$과 같은 방향이고, $z$-축은 기존의 $(0,-1,0)$과 같은 방향이다.


1.3.2 Euler’s Rotation Theorem

임의의 rotation은 좌표축에 대한 최대 세 개의 rotation으로 나타낼 수 있다. 이때, 같은 축에 대해 두 번 연속되는 rotation이 없어야 한다.


여기서 두 class의 rotation sequence가 등장한다.

  1. 하나의 특정한 축을 반복해서 사용.: $XYX, XZX, YXY, YZY, ZXZ, ZYZ$

  2. 모든 세 축을 사용.: $XYZ, XZY, YZX, YXZ, ZXY, ZYX$

예를 들어, $ZYZ$ sequence는

\[\textbf{R} = \textbf{R}_z(\phi)\textbf{R}_y(\theta)\textbf{R}_z(\psi) \tag{ $ 2 $ }\]

형태로 항공역학이나 동역학에서 자주 쓰이는 형태이다. Toolbox에서도 사용.


Robotics Toolbox - ZYZ Euler Angle

Euler angle은 3-vector $\mathbf{\Gamma} = (\phi, \theta, \psi)$.

Rotation matrix $\mathbf{\Gamma} = (0.1, 0.2, 0.3)$을 계산하고 싶다면,

R = rotz(0.1)) * roty(0.2) * rotz(0.3)
R = eul2r(0.1, 0.2, 0.3)

 R =

    0.9021   -0.3836   0.1977

    0.3875   0.9216   0.0198

    -0.1895   0.0587   0.9801


어느 쪽이든 같은 결과가 도출. 역방향을 계산하고 싶다면,

gamma = tr2eul(R)

 gamma =

    0.1000   0.2000   0.3000

또, 만약 $\theta$가 음수라면,

R = eul2r(0.1, -0.2, 0.3)
gamma = tr2eul(R)

 R =

    0.9021   -0.3836   -0.1977

    0.3875   0.9216   -0.0198

    0.1895   -0.0587   0.9801

 gamma =

    -3.0416   0.2000   -2.8416

$\theta$ 값은 양수로 나오는데다 $\phi$, $\psi$값은 이상한 값이 나온다. 그러나 이를 다시 Euler angle로 바꾸면,

eul2r( gamma )

 ans =

    0.9021   -0.3836   -0.1977

    0.3875   0.9216   -0.0198

    0.1895   -0.0587   0.9801

제대로 복구가 되는 모습을 볼 수 있다.

즉, 두 개의 다른 Euler angle set이 같은 rotation matrix를 가리킬 수 있다는 뜻! Rotation matrix에서 Euler angle로의 mappin은 유일하지 않으며, toolbox에서는 항상 $\theta$가 양수인 방향으로 return.


유사한 case로, $\theta=0$일 때,

R = eul2r( 0.1, 0, 0.3)

 R =

    0.9211   -0.3894   0

    0.3894   0.9211   0

    0   0   1.0000

역함수는

tr2eul(R)

 ans =

    0   0   0.4000


답이 이렇게 나오는 이유는 $\theta=0$일 때, $\textbf{R}_y = \textbf{I}$이므로, 식 $(2)$는

\[\textbf{R} = \textbf{R}_z(\phi) \textbf{R}_z(\psi) = \textbf{R}_z(\phi + \psi)\]

가 되기 때문이다. 따라서 이런 경우에 inverse operation은 별로 도움이 되지 않는다.

$\theta=0$인 경우를 singularity라고 한다.


ZYX Euler Angle

Roll, pitch, yaw. 이들을 $ZYX$ 또는 $XYZ$로 나타낸다. $ZYX$를 쓰면,

\[\textbf{R} = \textbf{R}_z(\theta_y)\textbf{R}_y(\theta_p)\textbf{R}_x(\theta_r) \tag{ $ 3 $ }\]

반대로 $XYZ$는

\[\textbf{R} = \textbf{R}_x(\theta_y)\textbf{R}_y(\theta_p)\textbf{R}_z(\theta_r) \tag{ $ 4 $ }\]


Robotics Toolbox - ZYX Angle

Toolbox는 기본적으로 $ZYX$를 사용하지만, ‘xyz’ 옵션이 존재.

R = rpy2r(0.1, 0.2, 0.3)

 R =

    0.9363   -0.2751   0.2184

    0.2896   0.9564   0.0370

    -0.1987   0.0978   0.9752

gamma = tr2rpy(R)

 gamma =

    0.1000   0.2000   0.3000


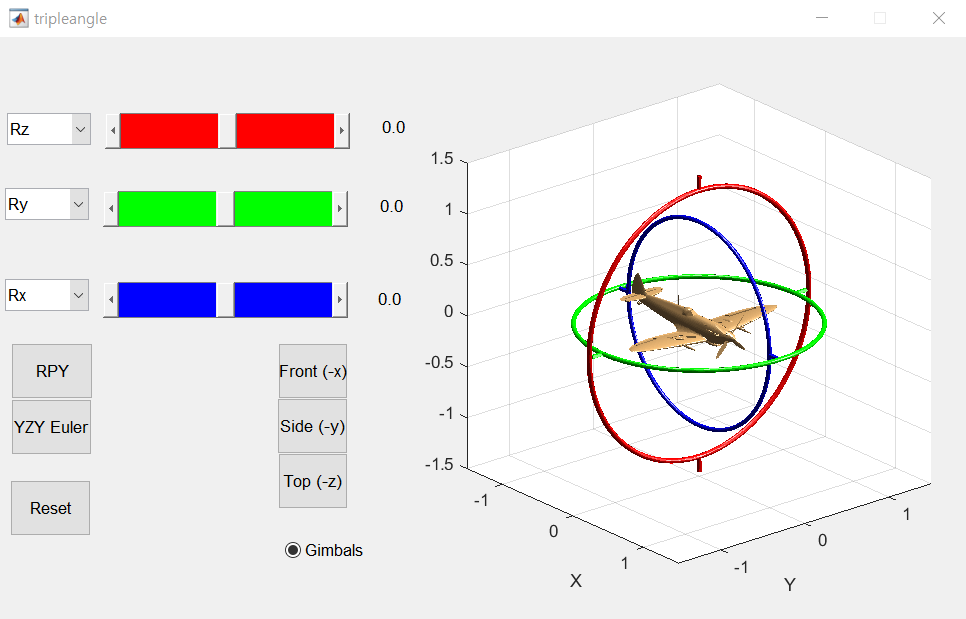
Robotics Toolbox - tripleangle

Euler angle과 roll-pitch-yaw angle을 실험할 수 있는 툴박스.

tripleangle



1.3.3 Sigularities and Gimbal Lock

Euler angle representation의 문제 중 하나는 singularity. Gimbal lock이라고도 한다. 이 현상은 angle sequence의 가운데 성분 때문에 발생한다.


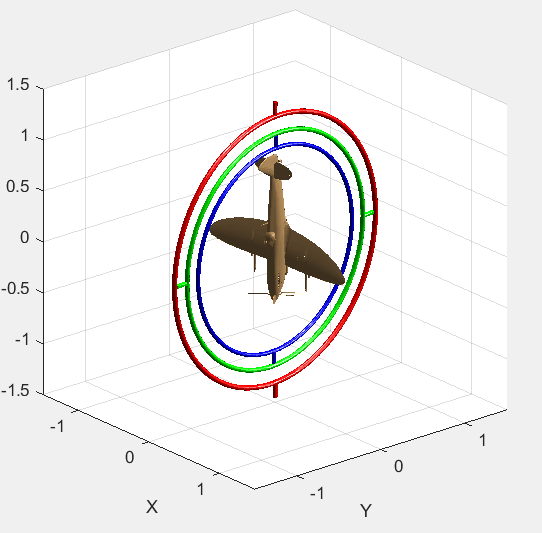
가운데 gimbal이 $90^{\circ}$를 이룬다고 하자. 그러면 안쪽 gimbal과 바깥쪽 gimbal의 축이 일치하게 되고, 이제 가능한 회전축이 두 개로 줄어들게 된다.2


수학적으로 표현해보자. $ZYX$- angle로 표현한 platform frame $\{A \}$에 대한 비행기의 body-fixed frame $\{B \}$는

\[{}^A \textbf{R}_B = \textbf{R}_Z(\alpha)\textbf{R}_Y(\beta)\textbf{R}_X(\gamma)\]

Matrix multiplication으로 어찌저찌 계산하면,

\[{}^A \textbf{R}_B = {}^A \textbf{R}_B(\alpha, \beta, \gamma) = \\ \begin{bmatrix} c \alpha c \beta & c \alpha s \beta s \gamma - s \alpha c \gamma & c \alpha s \beta c \gamma + s \alpha s \gamma \\ s \alpha c \beta & s \alpha s \beta s \gamma + c \alpha c \gamma & s \alpha s \beta c \gamma - c \alpha s \gamma \\ -s\beta & c \beta s \gamma & c \beta c \gamma \end{bmatrix}\]

여기서 $c \alpha$는 $\cos{\alpha}$, $s \beta$는 $\sin{\beta}$를 줄여서 쓴 것.


Gimbal lock이 발생하는 경우는 두 번째 gimbal의 각도 $\beta = 90^{\circ}$인 경우. 이 때 $c \beta = 0$, $s \beta = 1$이고, 위 행렬은

\[{}^A \textbf{R}_B = \begin{bmatrix} 0 & c \alpha s \gamma - s \alpha c \gamma & c \alpha c \gamma + s \alpha s \gamma \\ 0 & s \alpha s \gamma + c \alpha c \gamma & s \alpha c \gamma - c \alpha s \gamma \\ -1 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & -s(\alpha - \gamma) & c(\alpha - \gamma) \\ 0 & c(\alpha - \gamma) & s(\alpha - \gamma) \\ -1 & 0 & 0 \\ \end{bmatrix}\]


즉, $(\alpha - \gamma)$만이 정의된다. 이걸로는 $\alpha$, $\gamma$의 값이 각각 어떤지 알 수 없어진다. 둘 사이의 관계만 알 수 있을 뿐.


R = rpy2r(10, 90, 30);  % roll, pitch, yaw가 각각 10, 90, 30도인 rotation matrix
tr2rpy(R) % rotation matrix를 다시 Euler angle로 변환

 ans =

    32.9578   63.3798   98.8734


  1. 만일 deg 단위로 나온다면, MATLAB의 홈 > 경로 설정에서 MATLAB\Toolbox\phased 폴더를 맨 아래로 내린다. 여기에도 rotx가 있기 때문에 이 폴더에 있는 함수를 먼저 사용하게 된 것.
    함수가 어디 있는지 알고 싶다면 which 명령어를 사용한다.
    which rot x ↩

  2. 이를 '자유도(degree of freedom)가 하나 줄었다'고 말한다. ↩

You may also enjoy