2.2 Softmax Regression

새 무기를 산 지훈이는 못 가 봤던 던전에 도전할 수 있게 되었다. 이 던전은 몬스터가 무한으로 등장하며 죽기 전까지 버틴 시간과 토벌한 몬스터의 수를 토대로 A부터 C까지의 랭크를 부여한다.

Time ($x_1$)	Killed ($x_2$)	Rank ($y$)
10	7	A
8	5	A
4	5	B
3	3	B
2	4	B
2	2	C
12	1	C

---

2.2.1 Logistic Regression Returns

Sec 2.1의 Logistic regression을 그림으로 표현하면 다음과 같다.

Input $X$가 들어오면 weight $W$를 갖는 unit 내에서 계산한다. 그 결과가 $z$이고, 이 $z$를 sigmoid function에 통과시켜 $0$과 $1$ 사이의 값을 갖는 $\overline{Y}$를 얻는다. 이때 $Y$는 real value, $\overline{Y}$는 predictive value를 말한다.

Logistic regression을 직관적으로 보면, 다음과 같은 데이터들이 있을 때 이들을 분류해낼 수 있는 line을 학습시키는 것과 같다.

---

2.2.1 Multinomial Logistic Regression

자, 이번에는 지훈이의 클리어 실적으로부터 랭크를 분류해보도록 하자. 그래프를 그리면 다음과 같은 모습일 것이다.

이들을 어떻게 분류할 것인가?

Linear regression을 떠올리자면 먼저 $A$이거나 $A$가 아닌 case로 나눌 수 있겠다. 이에 따른 model이 하나 만들어질 것이다.

그럼 $B$인지 아닌지 분류할 수 있는 model도, $C$인지 아닌지 분류할 수 있는 model도 있겠다.

각각의 linear regression model에서 input data는 다음과 같은 계산을 거친다.

\[\begin{bmatrix} w_1 & w_2 & w_3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} w_1x_1 + w_2x_2 + w_3x_3 \end{bmatrix}\]

3개의 model이 있으므로, 우리는 이를 행렬곱을 사용해 표현할 수 있다.

\[\begin{bmatrix} w_{A1} & w_{A2} & w_{A3} \\ w_{B1} & w_{B2} & w_{B3} \\ w_{C1} & w_{C2} & w_{C3} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} w_{A1}x_1 + w_{A2}x_2 + w_{A3}x_3 \\ w_{B1}x_1 + w_{B2}x_2 + w_{B3}x_3 \\ w_{C1}x_1 + w_{C2}x_2 + w_{C3}x_3 \end{bmatrix} = \begin{bmatrix} \overline{y}_A \\ \overline{y}_B \\ \overline{y}_C \end{bmatrix}\]

이렇게 하면 세 logistic regression들이 마치 독립적으로 동작하는 것과 같은 형태의 model을 얻을 수 있다.

그런데 이렇게 하면 각 model마다 sigmoid를 한 번씩, 총 세 번이나 계산해야 하니 조금 오래 걸릴 것 같다. 보다 효율적인 방법이 있을 것이다.

---

2.2.1 Softmax Classifier

Sec 2.1의 마지막 부분을 떠올려 보자. 우리는 logistic regression model의 evaluation을 위해 x_train값을 우리가 만든 모델에 집어넣어 0에서 1 사이의 확률값을 얻었다.

Multinomial의 경우에도 이런 결과가 나올 수 있으면 좋겠다. $\overline{y}_A$는 높은 값이, $\overline{y}_B$와 $\overline{y}_C$는 낮은 값이 나오게 된다면 해당 case를 A랭크로 분류할 수 있을 텐데.

데이터의 결과값 $\overline{y}$를 0과 1 사이의 확률적인 값으로 바꾸어주는 함수가 바로 Softmax이다. 즉, multinomial case에서 sigmoid와 같은 역할을 하는 녀석이다.

Softmax의 정의는 다음과 같다.

\[S(y_i) = \frac{e^{y_i}}{\sum_j e^{y_j}}\]

즉 전체 값으로 해당 값을 나눈 것과 같다.

마지막으로 One-Hot Encoding을 사용하여 가장 큰 값을 $1$로, 나머지를 $0$으로 만들어 주면 끝이 난다.

직접 계산해도 되지만 Pytorch에는 softmax function이 존재한다.

 - softmax : dim은 softmax가 계산되는 차원. dim에 해당하는 slice에 대해서 합이 1이 된다.
---
- Result : 

tensor([0.0900, 0.2447, 0.6652])

tensor(1.)

---

2.2.2 Cross Entropy

이제 cost function만 해결하면 되겠다. Cost function은 우리가 예측한 값과 실제 값이 얼마나 차이가 나는지를 알려주는 지표였다. 이 cost function이 최소화가 되면 학습이 끝나는 것이었다.

예측값과 실제값의 비교를 위해 다음 형태의 cross entropy 함수를 사용한다.

여기서 $\overline{Y} = S(Y)$는 예측값, $L=Y$는 label, 즉 실제 값을 의미한다.

Cross entropy가 어떻게 cost function의 역할을 하는지 보자. 식을 정리하면

\[-\sum_i L_i \log(\overline{y}_i) = \sum_i L_i \ast (-\log(\overline{y}_i))\]

이고, $\overline{y}_i$는 0에서 1 사이의 값을 가진다. 이때 $-\log(\overline{y}_i)$의 값은 다음과 같다.

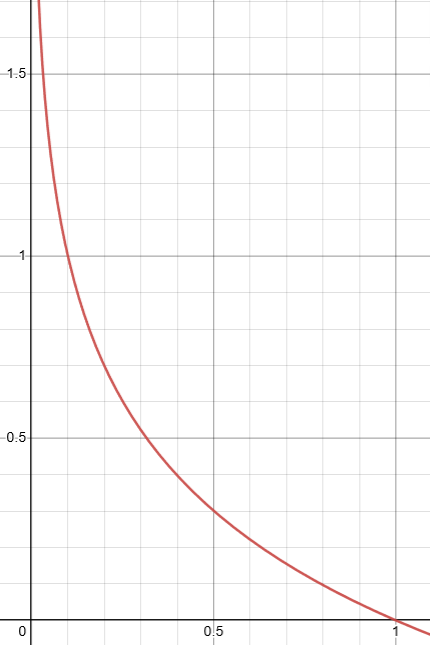
그러므로 $Y$의 예측값에 의한 $\log$ 데이터 행렬에 실제 값을 곱하게 되면, cost function이 커질 때 예측이 틀리고 작아질 때 예측이 맞는 결과가 나타난다.

Logistic regression의 경우를 다시 생각해 보자. Logistic cost는 다음과 같았다.

\[c(H(x),y) = y \log(H(x))-(1-y)\log(1-H(x))\]

Logistic regression은 하나의 데이터에 대한 binary classification이므로, $y$가 0일 때와 1일 때만을 생각하면 된다. 그래서 $y$와 $1-y$를 사용했던 것. 즉, logistic cost는 cross entropy의 특별한 case였던 것이다.

이제 cost가 완성되었으니 training set에 대한 평균을 취하면 loss를 얻는다.

\[\mathcal{L} = \frac{1}{N} \sum_i D(S(Wx_i + b), L_i)\]

만일 gradient descent를 이용하고자 하면 위 함수를 미분하면 되겠다.

Low-level에서 cross entropy loss를 계산해 보자.

 - dim=1이므로, 각 행의 합이 1이 되도록 softmax를 취한다.
---
 - Result : 

tensor([[0.1673, 0.2409, 0.5161, 0.0681, 0.6781],
        [0.2962, 0.2215, 0.5359, 0.0104, 0.1005],
        [0.6030, 0.5795, 0.6532, 0.0886, 0.8187]], requires_grad=True)
tensor([[0.1648, 0.1775, 0.2337, 0.1493, 0.2747],
        [0.2095, 0.1945, 0.2663, 0.1574, 0.1723],
        [0.2055, 0.2007, 0.2161, 0.1228, 0.2549]], grad_fn=<SoftmaxBackward0>)
tensor([1, 0, 3])

위 예시에서 class의 수는 5개, sample은 3개이다. 실제 값은 텐서 $y$의 index값이라고 하자. 즉 실제 값은 각 행의 1, 0, 3번째 index에 들어있는 값인 0.1775, 0.2095, 0.1228이다.

One-Hot vector로 나타내자. 실제 값과 일치하면 1, 그렇지 않으면 0이 될 것이다.

 - numpy.zeros_like : 특정 array와 같은 크기의 zero matrix를 만든다.
 - unsqueeze : 값이 1인 dim을 끼워넣는다. 이때 인자는 끼워넣을 index.
 - torch.scatter_(dim, index, src) : index가 가리키는 위치에 특정 값을 대입한다. dim은 index가 적용되는 방향이다. 0은 행, 1은 열이 바뀌는 방향으로 이동한다. 
 - unsqueeze : 값이 1인 dim을 끼워넣는다. 이때 인자는 끼워넣을 index. (3, )의 크기였던 텐서 y가 (3, 1)이 된다. 즉, 

 tensor([[1],
        [0],
        [3]])
---
 - Result : 

tensor([[0., 1., 0., 0., 0.],
        [1., 0., 0., 0., 0.],
        [0., 0., 0., 1., 0.]])

tensor(1.7963, grad_fn=<MeanBackward0>)

High-level에서도 해 보자. softmax 함수의 log를 log_softmax로, cost function을 nll_loss로 간략하게 할 수 있다. 여기서 nll은 negative log likelihood를 뜻한다.

게다가 둘을 합쳐서 한번에 cross_entropy로 계산할 수도 있다.

 - Result : 

tensor([[-1.8027, -1.7291, -1.4539, -1.9019, -1.2919],
        [-1.5629, -1.6375, -1.3232, -1.8487, -1.7586],
        [-1.5825, -1.6060, -1.5322, -2.0968, -1.3667]],
       grad_fn=<LogSoftmaxBackward0>)

tensor(1.7963, grad_fn=<NllLossBackward0>)

tensor(1.7963, grad_fn=<NllLossBackward0>)

---

2.2.3 Training with Cross Entropy Loss

자, 이제 training을 시작해 보자. A랭크를 2, B랭크를 1, C랭크를 0이라는 값으로 생각하기로 하고 학습하자. 다음은 각각 low-level 코드의 cross_entropy 함수를 사용한 학습 코드이다. 결과는 같다.

 - Result : 

Epoch    0/1000 Cost: 1.098612
Epoch  100/1000 Cost: 0.451352
Epoch  200/1000 Cost: 0.429448
Epoch  300/1000 Cost: 0.422606
Epoch  400/1000 Cost: 0.419385
Epoch  500/1000 Cost: 0.417534
Epoch  600/1000 Cost: 0.416335
Epoch  700/1000 Cost: 0.415494
Epoch  800/1000 Cost: 0.414870
Epoch  900/1000 Cost: 0.414386
Epoch 1000/1000 Cost: 0.413999

High-level 상에서는 다음과 같다.

 - Result : 

Epoch    0/1000 Cost: 2.790699
Epoch  100/1000 Cost: 0.354288
Epoch  200/1000 Cost: 0.276122
Epoch  300/1000 Cost: 0.230974
Epoch  400/1000 Cost: 0.200142
Epoch  500/1000 Cost: 0.177557
Epoch  600/1000 Cost: 0.160222
Epoch  700/1000 Cost: 0.146444
Epoch  800/1000 Cost: 0.135187
Epoch  900/1000 Cost: 0.125784
Epoch 1000/1000 Cost: 0.117789