2.1 Logistic Regression
사냥을 끝낸 지훈이는 무기를 새로 장만하고 싶다. 승현이는 때마침 지훈이가 원하는 무기를 가지고 있었다. 두 사람은 채팅창으로 흥정을 시작한다.
지훈이가 200원을 부르자 승현이는 팔지 않겠다고 했다. 300원을 불렀을 때도 팔지 않겠다고 했다. 700원을 부르자 비로소 팔겠다고 말했다. 600원을 불렀을 때도 팔겠다고 했다.
| Price ($x$) | Deal ($y$) |
|---|---|
| 200 | 0 |
| 300 | 0 |
| 400 | 0 |
| 500 | 1 |
| 600 | 1 |
| 700 | 1 |
Binary Classification이란 데이터를 두 카테고리 중에서 어디에 속하는지 분류하는 것을 말한다. 이메일을 스팸메일과 그렇지 않은 것으로, 공항 입국자를 내국인과 외국인으로, 커피를 카페인과 디카페인으로 분류하는 등이 이에 속한다.
즉, 예측값이 discrete하다면 classification, continuous하다면 regression.
이러한 분류 과정을 학습하기 위해 0과 1로 인코딩하자. 지훈이가 제시한 금액과 거래 성공 여부를 판단하는 모델을 만들자.
Ch.1 에서 사용한 linear regression을 사용해 보자. 그러면 0.5를 기준으로 이보다 크면 success, 낮으면 fail이 되도록 분류하는 알고리즘을 생각할 수 있다.
그런데 문제가 있다. 첫째는 linear regression 때문에 예측값이 실제와 다르게 나온다는 점이다. 500원을 제시해도 700원을 제시해도 실제 거래는 성사하지만 예측값은 0에서 1 사이의 값이 나오게 된다.
두 번째 문제는… 만약 지훈이가 실수로 0을 하나 더 쳐서 거래창에 5000원을 올려버렸다고 해 보자. 승현이는 당연히 옳다구나 거래를 받아들일 것이다.
Linear regression은 5000원을 제시했을 때 success인 1의 값을 가지게 된다. 이대로 데이터를 학습시킨다면 기울기가 낮아지게 되고, 0.5를 기준으로 다시 판별하게 되면 실제로 거래가 성공할 수 있는데도 실패로 판별될 수가 있다. 세상에.
2.1.1 Logistic Hypothesis
Logistic regression에서는 위와 같은 경우를 해결하기 위해 선형 함수가 아니라 sigmoid function을 도입한다.
\[\sigma(x) = \frac{1}{1+e^{-x}}\]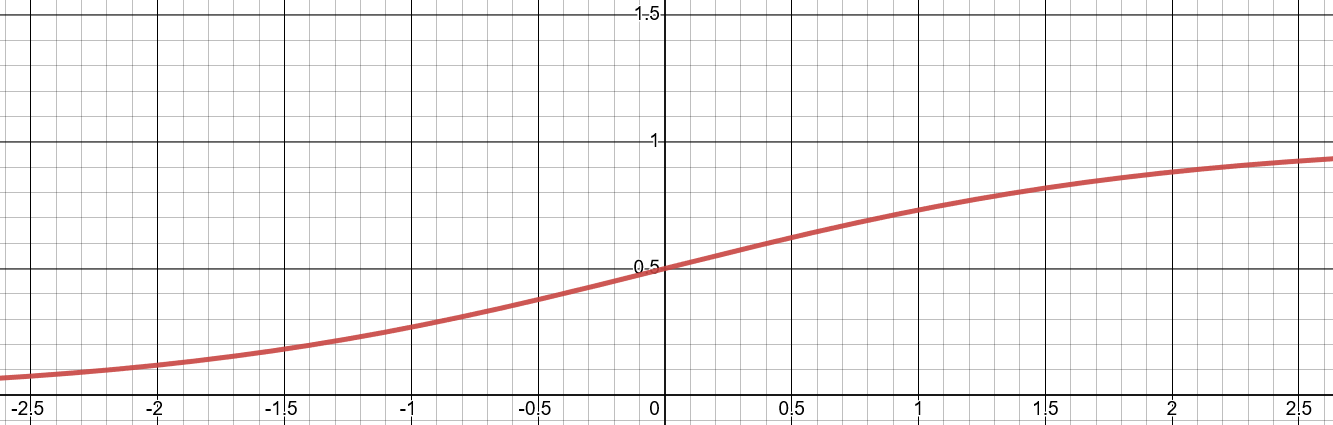
이를 사용해 logistic hypothesis를 다음과 같이 정의하자.
\[H(X) = \frac{1}{1+e^{-W^TX}}\]weight의 형태에 따라 $-W$ 대신 $W$를 써도 무방.
2.1.2 Cost of Logistic Regression
Cost function은 다음과 같이 계산할 수 있었다.
\[cost(W, b) = \frac{1}{m} \sum_{i=1}^m (H(x^{(i)}) - y^{(i)})^2\]그러므로 linear regression의 경우 cost function은 이차식 형태가 되고, global minimum이 존재하게 된다. 그런데 위 식으로 logistic regression의 cost를 계산하면 그렇게 깔끔한 모습이 나오지는 않는다.
더이상 linear한 식이 아니기 때문. 이렇게 local minimum들이 잔뜩 존재하는 함수에서 평범하게 gradient descent를 적용할 수야 없다.
Cost function도 적절하게 바꾸자.
\[cost(W, b) = \frac{1}{m} \sum c(H(x),y)\] \[c(H(x),y) = \begin{cases} -\log(H(x)) & :y=1\\ -\log(1-H(x)) & :y=0 \end{cases}\]기본적인 아이디어는 다음과 같다. $y=1$일 때를 생각해 보자면, cost function을 최소화시키기 위해서는 예측값이 1에 가까워져야 한다. 반대로 $y=0$에서는 예측값이 0에 가까워져야 한다.
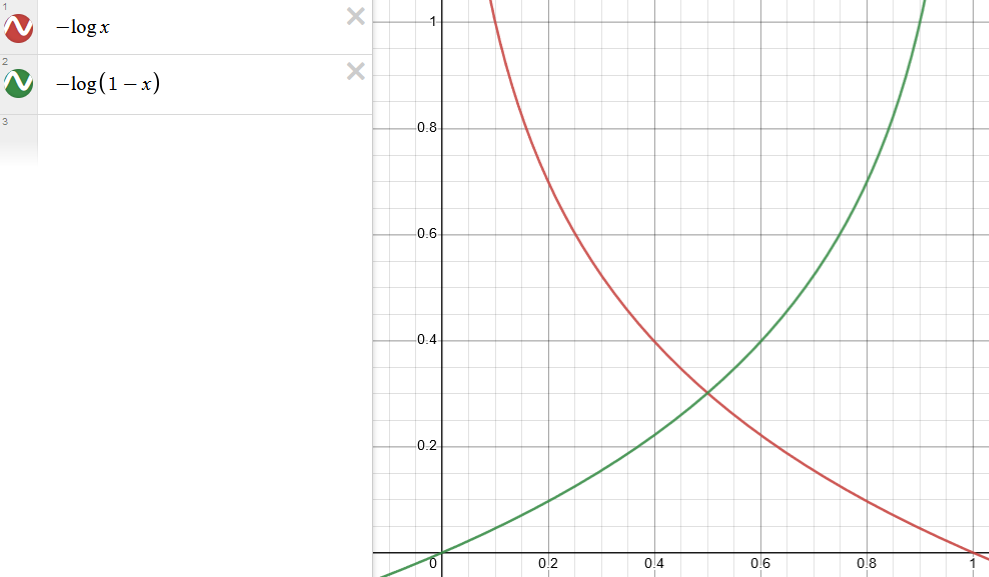
두 case를 하나의 식으로 나타내면 다음 cost function이 만들어진다.
\[c(H(x),y) = y \log(H(x))-(1-y)\log(1-H(x))\]자, 이제 gradient descent를 사용할 수 있게 되었다.
\[W := W - \alpha \frac{\partial}{\partial W} cost(W)\] - manual_seed : random seed를 고정시킨다.
- sigmoid : pytorch에는 sigmoid function이 내장.
- mean : 평균을 취하는 함수.
위에서 적은 수식들을 한 번에 해결하는 방법이 있다. 위 식에 해당하는 cost function을 Binary Cross Entropy(BCE)라고 한다. BCE를 이용해 학습을 진행해 보자.
- binary_cross_entropy() : BCE
---
- Result :
Epoch 0/1000 Cost: 0.693147
Epoch 100/1000 Cost: 0.177910
Epoch 200/1000 Cost: 0.116810
Epoch 300/1000 Cost: 0.099188
Epoch 400/1000 Cost: 0.087217
Epoch 500/1000 Cost: 0.078322
Epoch 600/1000 Cost: 0.071342
Epoch 700/1000 Cost: 0.065658
Epoch 800/1000 Cost: 0.060907
Epoch 900/1000 Cost: 0.056857
Epoch 1000/1000 Cost: 0.053350
이제 train이 끝났다. model이 얼마나 training set에 잘 들어맞는지 체크하자. 기존의 dataset을 모델에 집어넣어 보자.
- Result :
tensor([[1.4644e-04],
[5.2484e-03],
[1.5970e-01],
[8.7255e-01],
[9.9596e-01],
[9.9989e-01]], grad_fn=<SigmoidBackward0>)
이제 hypothesis가 0.5보다 크거나 같으면 true로 정의하는 binary prediction을 만들자. 정확한 값인 y_train과 비교해 보자.
- Result :
tensor([[False],
[False],
[False],
[ True],
[ True],
[ True]])
tensor([[0.],
[0.],
[0.],
[1.],
[1.],
[1.]])
tensor([[True],
[True],
[True],
[True],
[True],
[True]])
2.1.3 Higher Implementation
다음은 nn.Module 추상 클래스를 상속받아 logistic regression model을 만드는 클래스이다. 실제 구현에는 이런 방식을 많이 사용한다.
- BinaryClassifier(nn.Module) : 클래스 선언 시 상속할 부모 클래스의 이름을 괄호 내에 적는다.
- super().__init__() : 초기화 단계에서 부모 클래스의 __init__ 메소드 호출. 부모 클래스에 전달할 input이 있다면 괄호 내에 적는다.
- self.linear : weight W의 역할을 한다.
- self.sigmoid : bias b의 역할을 한다.
이를 토대로 진행한 결과이다.
- Result :
Epoch 0/1000 Cost: 0.740465 Accuracy 50.00
Epoch 100/1000 Cost: 0.169962 Accuracy 83.33
Epoch 200/1000 Cost: 0.115382 Accuracy 100.00
Epoch 300/1000 Cost: 0.098269 Accuracy 100.00
Epoch 400/1000 Cost: 0.086555 Accuracy 100.00
Epoch 500/1000 Cost: 0.077813 Accuracy 100.00
Epoch 600/1000 Cost: 0.070933 Accuracy 100.00
Epoch 700/1000 Cost: 0.065321 Accuracy 100.00
Epoch 800/1000 Cost: 0.060622 Accuracy 100.00
Epoch 900/1000 Cost: 0.056611 Accuracy 100.00
Epoch 1000/1000 Cost: 0.053136 Accuracy 100.00




