2.3 Algebra of Sets
"합집합, 교집합, 그리고 또..."
우리가 가지고 있는 연산들,
\[\begin{align*} \textrm{Union : }A \cup B &= \{ x \ |\ x \in A \vee x \in B\} \\ \textrm{Intersection : }A \cap B &= \{ x \ |\ x \in A \wedge x \in \} \\ \textrm{Relative complement : }A - B &= \{ x \in A \ |\ x \notin B\} \end{align*}\]Remark 2.3.1
$A \cup B$는 Union Axiom으로부터 얻어지지만,
$A \cap B$와 $A-B$는 Subset Axiom으로부터 얻어진다.
주의할 점.
$B$의 absolute complement, 즉 $\{ x |\ x \notin B\}$는 set으로 만들 수 없다. 이를 $B$와 union하면 모든 set들의 class가 되기 때문.
Proposition 2.3.2 [Commutative Laws]
\[\begin{align*} A \cup B &= B \cup A \\ A \cap B &= B \cap A \\ \end{align*}\]Proposition 2.3.3 [Associative Laws]
\[\begin{align*} A \cup (B \cup C) &= (A \cup B) \cup C \\ A \cap (B \cap C) &= (A \cap B) \cap C \\ \end{align*}\]Proposition 2.3.4 [Distributive Laws]
\[\begin{align*} A \cap (B \cup C) &= (A \cap B) \cup (A \cap C) \\ A \cup (B \cap C) &= (A \cup B) \cap (A \cup C) \\ \end{align*}\]Proposition 2.3.5 [De Morgan’s Laws]
\[\begin{align*} C-(A \cup B) &= (C-A) \cap (C-B) \\ C-(A \cap B) &= (C-A) \cup (C-B) \\ \end{align*}\]Proposition 2.3.6 [Identities Involving $\varnothing$]
\[\begin{align*} A \cup \varnothing &= A \\ A \cap \varnothing &= \varnothing \\ A \cap (C-A) &= \varnothing \\ \end{align*}\]보통 우리가 고려하는 set들은 어떤 큰 set 또는 space $S$의 subset이다.
$A$, $B$가 $S$의 subset이라고 가정하면, 고정된 set $S$에 대해 $S-A$를 $-A$라고 줄여서 쓸 수 있다. 그러면 De Morgan’s Law는 다음 형태가 된다.
\[\begin{align*} -(A \cup B) &= -A \cap -B \\ -(A \cap B) &= -A \cup -B \\ \end{align*}\]또, 다음 관계식 역시 성립.
\[\begin{align*} A \cup S &= S \\ A \cap S &= A \\ A \cup -A &= S \\ A \cap -A &= \varnothing \\ \end{align*}\]이제 법칙들을 증명할 차례다. 예시로 다음 distributive law를 생각.
\[A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\]증명 방법 중 하나는 직접 그림을 그리는 것.
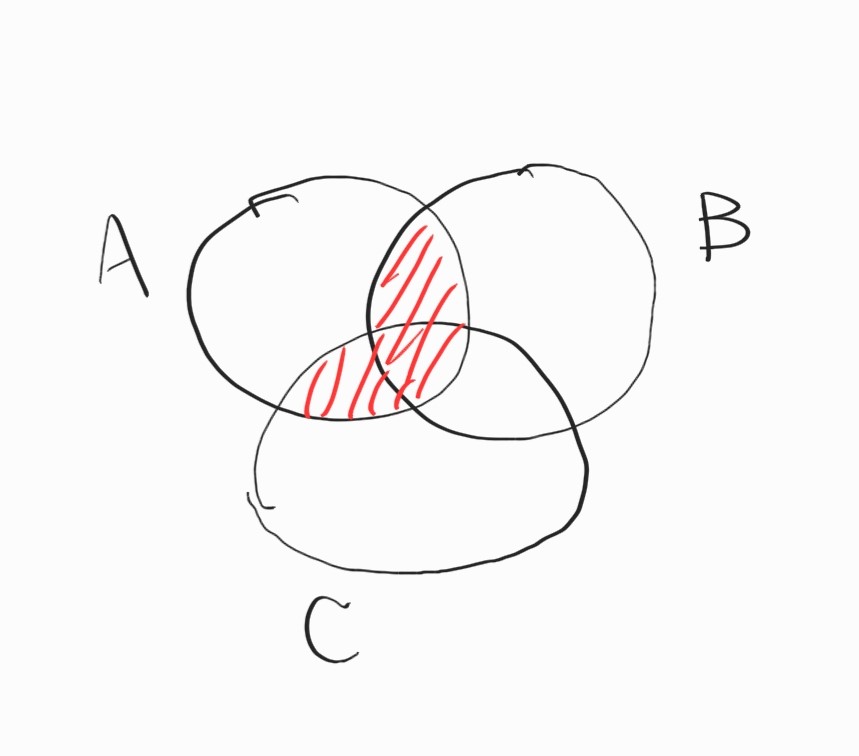
양변의 두 식이 같은 영역을 가리킨다. …진짜로?
그림 없이 해 보자. 임의의 $x$에 대하여
\[x \in A \cap (B \cup C) \Leftrightarrow x \in (A \cap B) \cup (A \cap C)\]임을 보이면 된다.1 아무튼 임의의 $x$를 생각하자. 이 $x$가 $A$에 있는지 없는지, $B$에 있는지 없는지는 모르지만 8가지 가능성이 존재한다.
\[\begin{align*} x \in A \qquad x \in B \qquad x \in C \\ x \in A \qquad x \in B \qquad x \notin C \\ x \in A \qquad x \notin B \qquad x \in C \\ x \in A \qquad x \notin B \qquad x \notin C \\ x \notin A \qquad x \in B \qquad x \in C \\ x \notin A \qquad x \in B \qquad x \notin C \\ x \notin A \qquad x \notin B \qquad x \in C \\ x \notin A \qquad x \notin B \qquad x \notin C \\ \end{align*}\]이들은 그림의 8개 영역을 나타낸다. 그러면 이 8개 case에 대해
\[x \in A \cap (B \cup C) \Leftrightarrow x \in (A \cap B) \cup (A \cap C)\]를 확인하면 된다. 예를 들어, case 5는
\[x \notin A \cap (B \cup C) \wedge x \notin (A \cap B) \cup (A \cap C)\]가 된다.
이 방법은 어느 equation이라도 적용 가능. $n$개의 letter가 있으면, $ 2^n $개 case를 확인하면 된다.
Example 2.3.7
Inclusion relation에 대해서는 다음 monotonicity 성질을 얻는다.
\[\begin{align*} A \subseteq B &\Rightarrow A \cup C \subseteq B \cup C \\ \\ A \subseteq B &\Rightarrow A \cap C \subseteq B \cap C \\ \\ A \subseteq B &\Rightarrow \bigcup A \subseteq \bigcup B \\ \end{align*}\]다음 antimonotonicity도 잊지 말자.
\[\begin{align*} A \subseteq B &\Rightarrow C-B \subseteq C-A \\ \\ \varnothing \not= A \subseteq B &\Rightarrow \bigcap B \subseteq \bigcap A \\ \end{align*}\]증명은 간단하니 생략.
지금부터는 임의의 union/intersection을 포함하는 등식들.
Proposition 2.3.8 [Distributive Laws]
\[\begin{align*} A \cup \bigcap \mathcal{B} &= \bigcap \{A \cup X \ |\ X \in \mathcal{B}\} \textrm{ for } \mathcal{B} \not= \varnothing \\ \\ A \cap \bigcup \mathcal{B} &= \bigcup \{A \cap X \ |\ X \in \mathcal{B}\} \end{align*}\]우변의 notation은 abstraction의 확장.
Set $\{A \cup X |\ X \in \mathcal{B}\}$ 는 $\mathcal{B}$ 안의 어떤 $X$에 대해, $A \cup X$ 형태의 set들을 정확히 member로 갖는 유일한 set $\mathcal{D}$.
\[t \in \mathcal{D} \qquad \Leftrightarrow \qquad t = A \cup X \textrm{ for some } X \textrm{ in } \mathcal{B}\]그러한 set $\mathcal{D}$의 존재성은 $A \cup X \subseteq \bigcup \mathcal{B}$로부터 얻는다. $\mathcal{D}$는 $\mathcal{P}(A \cup \bigcup B)$의 subset이고, subset axiom에 의해
\[\{t \in \mathcal{P}(A \cup \bigcup \mathcal{B}) \ |\ t = A \cup X \textrm{ for some } X \textrm{ in } \mathcal{B}\}\]이고, 이는 정확히 $\mathcal{D}$.
Example 2.3.9
Set $\mathcal{A}$와 $C$에 대해,
\[\{ C-X \ |\ X \in \mathcal{A} \}\]는 $\mathcal{A}$의 member들의 relative complement들의 set. 즉, 임의의 $t$에 대해
\[t \in \{ C-X \ |\ X \in \mathcal{A} \} \quad \Leftrightarrow \quad t=C-X \textrm{ for some } X \in \mathcal{A}\]또한, $\{ \mathcal{P}(X) |\ X \in \mathcal{A} \}$는
\[t \in \{ \mathcal{P}(X) \ |\ X \in \mathcal{A} \} \quad \Leftrightarrow \quad t=\mathcal{P}(X) \textrm{ for some } X \in \mathcal{A}\]Proposition 2.3.10 [De Morgan’s Laws (for $\mathcal{A} \not= \varnothing$)]
\[\begin{align*} C - \bigcup \mathcal{A} &= \bigcap \{ C-X \ |\ X \in \mathcal{A} \} \\ \\ C - \bigcap \mathcal{A} &= \bigcup \{ C-X \ |\ X \in \mathcal{A} \} \\ \end{align*}\]만약 $\bigcup \mathcal{A} \subseteq S$이면,
\[\begin{align*} -\bigcup \mathcal{A} &= \bigcap \{ -X \ |\ X \in \mathcal{A} \} \\ \\ -\bigcap \mathcal{A} &= \bigcup \{ -X \ |\ X \in \mathcal{A} \} \\ \end{align*}\]여기서 $-X$는 $S-X$.
Proof.
역방향으로 가면 ”$\Leftrightarrow$”를 얻을 수 있다. 이때는 $\mathcal{A} \not= \varnothing$ 조건이 필요하다! $\square$
Remark 2.3.11
편의상의 notation. 설명하지 않아도 알겠지만,
\[\begin{align*} \bigcap_{X \in \mathcal{B}} (A \cup X) \qquad &\textrm{for} \qquad \bigcap \{A \cup X \ |\ X \in \mathcal{B}\} \\ \\ \bigcup_{X \in \mathcal{B}} (C- X) \qquad &\textrm{for} \qquad \bigcup \{C- X \ |\ X \in \mathcal{B}\} \\ \end{align*}\]Exercise 2.3.12
다음은 동치.
\[\begin{align*} &(a) \quad A \subseteq B \\ \\ &(b) \quad A-B=\varnothing \\ \\ &(c) \quad A \cup B = B \\ \\ &(d) \quad A \cap B = A \\ \\ \end{align*}\]Proof.
[$(a) \Rightarrow (b)$] $A \subseteq B$이면, $A$에는 있으나 $B$에는 포함되지 않는 원소는 존재하지 않는다. 따라서 $A-B=\varnothing$.
[$(b) \Rightarrow (a)$] $A-B=\varnothing$이면, 임의의 $x \in A$는 반드시 $x \in B$여야 한다. 그러므로 $A \subseteq B$.
[$(a) \Rightarrow (c)$] $A \subseteq B$를 가정. 만약 $x \in A \cup B$이면, $x \in A$ 또는 $x \in B$이다.
$\Rightarrow$ $x \in B$ 또는 $x \in B$.
$\Rightarrow$ $x \in B$.
[$(c) \Rightarrow (a)$] $x \in A$이면 $x \in A \cup B$이고, monotonicity에 의해 $x \in A \cup B = B$.
[$(a) \Rightarrow (d)$] $A \subseteq B$를 가정.
$x \in A \cap B$이면 monotonicity에 의해 $x \in A$.
$x \in A$이면 가정에 의해 $x \in B$이고, 따라서 $x \in A \cap B$.
[$(d) \Rightarrow (a)$] $x \in A$이면, $x \in A \cap B$이고, monotonicity에 의해 $x \in B$.
$\square$
-
Extensionality! ↩
